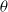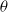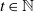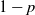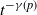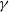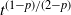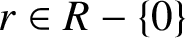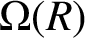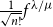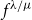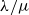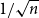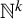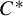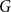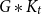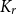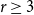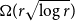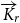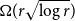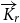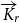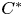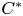Refine listing
Actions for selected content:
1718 results in 05xxx
Arcsine laws for random walks generated from random permutations with applications to genomics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 851-867
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Percolation phase transition in weight-dependent random connection models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1090-1114
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
On point processes defined by angular conditions on Delaunay neighbors in the Poisson–Voronoi Tessellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 952-965
- Print publication:
- December 2021
-
- Article
- Export citation
A stochastic matching model on hypergraphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 951-980
- Print publication:
- December 2021
-
- Article
- Export citation
Clustering in preferential attachment random graphs with edge-step
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 890-908
- Print publication:
- December 2021
-
- Article
- Export citation
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
ON THE STRONG METRIC DIMENSION OF A TOTAL GRAPH OF NONZERO ANNIHILATING IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 431-439
- Print publication:
- June 2022
-
- Article
- Export citation
FIRST-ORDER AXIOMATISATIONS OF REPRESENTABLE RELATION ALGEBRAS NEED FORMULAS OF UNBOUNDED QUANTIFIER DEPTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1283-1300
- Print publication:
- September 2022
-
- Article
- Export citation
STRUCTURAL CONSIDERATIONS OF RAMSEY ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1677-1692
- Print publication:
- December 2022
-
- Article
- Export citation
Extending the Tutte and Bollobás–Riordan polynomials to rank 3 weakly coloured stranded graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 507-549
-
- Article
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
Cocycles on groupoids arising from
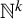 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN APERIODIC TILE WITH EDGE-TO-EDGE ORIENTATIONAL MATCHING RULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1727-1755
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On bucket increasing trees, clustered increasing trees and increasing diamonds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 13 October 2021, pp. 629-661
-
- Article
- Export citation
The critical window in random digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 411-429
-
- Article
- Export citation
New dualities from old: generating geometric, Petrie, and Wilson dualities and trialities of ribbon graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 07 October 2021, pp. 574-597
-
- Article
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
On deficiency problems for graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 478-488
-
- Article
- Export citation
Strong complete minors in digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 24 September 2021, pp. 489-506
-
- Article
- Export citation
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 20 September 2021, pp. 762-778
-
- Article
- Export citation