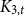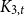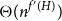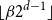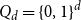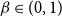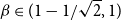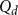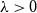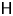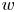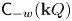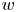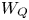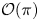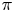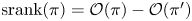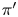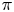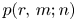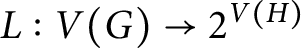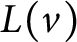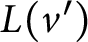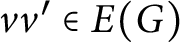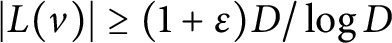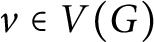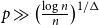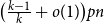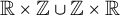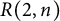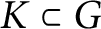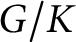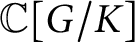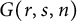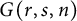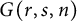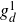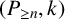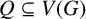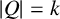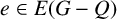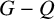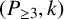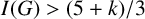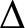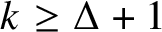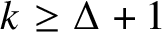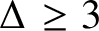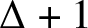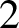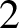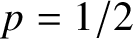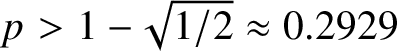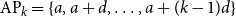Refine listing
Actions for selected content:
1718 results in 05xxx
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Subgraph densities in a surface
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 January 2022, pp. 812-839
-
- Article
- Export citation
Independent sets of a given size and structure in the hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 702-720
-
- Article
- Export citation
Functorially finite hearts, simple-minded systems in negative cluster categories, and noncrossing partitions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 23 February 2022, pp. 211-243
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some generating functions and inequalities for the andrews–stanley partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 120-135
-
- Article
- Export citation
Tuning as convex optimisation: a polynomial tuner for multi-parametric combinatorial samplers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 765-811
-
- Article
- Export citation
Independent transversals in bipartite correspondence-covers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 882-894
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A spanning bandwidth theorem in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 598-628
-
- Article
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
On the multiplication of spherical functions of reductive spherical pairs of type A
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 341-374
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomiality of factorizations in reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 245-266
- Print publication:
- February 2023
-
- Article
- Export citation
Tevelev degrees and Hurwitz moduli spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 479-510
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOUGHNESS, ISOLATED TOUGHNESS AND PATH FACTORS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 195-202
- Print publication:
- October 2022
-
- Article
- Export citation
Equitable colourings of Borel graphs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology of random
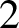 $2$-dimensional cubical complexes
$2$-dimensional cubical complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 November 2021, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Frucht property in the quantum group setting
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 603-633
- Print publication:
- September 2022
-
- Article
- Export citation
A blurred view of Van der Waerden type theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 26 November 2021, pp. 684-701
-
- Article
- Export citation
Random intersection graphs with communities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1061-1089
- Print publication:
- December 2021
-
- Article
- Export citation
Sequential metric dimension for random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 909-951
- Print publication:
- December 2021
-
- Article
- Export citation