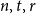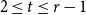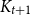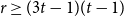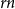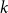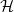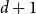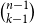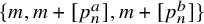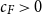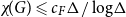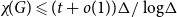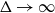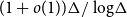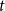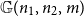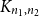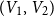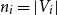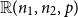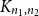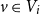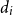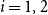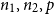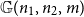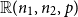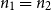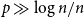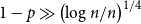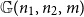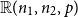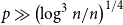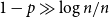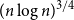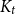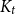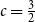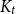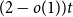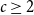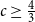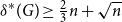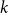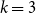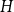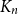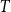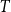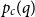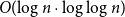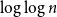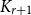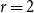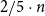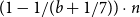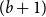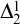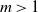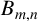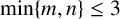Refine listing
Actions for selected content:
1718 results in 05xxx
Complete subgraphs in a multipartite graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1092-1101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-tree counts on hyperbolic random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1032-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Undecidability of the Spectral Gap
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 June 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hypergraphs without non-trivial intersecting subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1076-1091
-
- Article
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colouring graphs with forbidden bipartite subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 June 2022, pp. 45-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sandwiching biregular random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves – CORRIGENDUM
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 337-339
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Improved lower bound for the list chromatic number of graphs with no Kt minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1070-1075
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1031-1047
-
- Article
- Export citation
On tripartite common graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 May 2022, pp. 907-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The diameter of the uniform spanning tree of dense graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1010-1030
-
- Article
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The chromatic profile of locally colourable graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 976-1009
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TREE FORCING AND DEFINABLE MAXIMAL INDEPENDENT SETS IN HYPERGRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 1419-1458
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of tree parameters by martingale approach
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 737-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Giant descendant trees, matchings, and independent sets in age-biased attachment graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 299-324
- Print publication:
- June 2022
-
- Article
- Export citation
Counting H-free orientations of graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 79-95
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE SINGULARITY OF ORIENTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 357-362
- Print publication:
- December 2022
-
- Article
- Export citation