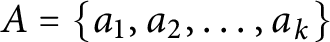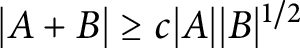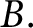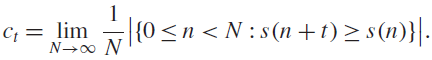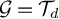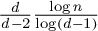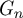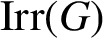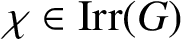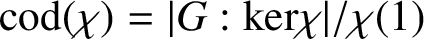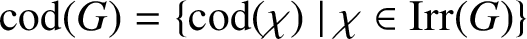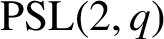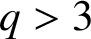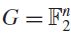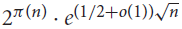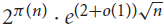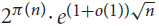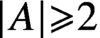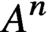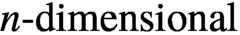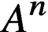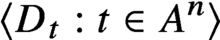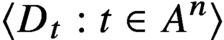Refine listing
Actions for selected content:
1718 results in 05xxx
On symmetric intersecting families of vectors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 18 March 2021, pp. 899-904
-
- Article
- Export citation
A proof of a conjecture of Gyárfás, Lehel, Sárközy and Schelp on Berge-cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 09 March 2021, pp. 654-669
-
- Article
- Export citation
The fluid limit of a random graph model for a shared ledger
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 81-106
- Print publication:
- March 2021
-
- Article
- Export citation
Instantons and Bar-Natan homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 484-528
- Print publication:
- March 2021
-
- Article
- Export citation
Sumsets of semiconvex sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 84-94
- Print publication:
- March 2022
-
- Article
- Export citation
Simple peeling of planar maps with application to site percolation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 907-941
- Print publication:
- August 2022
-
- Article
- Export citation
Scale-free percolation in continuous space: quenched degree and clustering coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 106-127
- Print publication:
- March 2021
-
- Article
- Export citation
On a generalization of the Rényi–Srivastava characterization of the Poisson law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 68-82
- Print publication:
- March 2021
-
- Article
- Export citation
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
RAMSEY’S COHEIRS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 377-391
- Print publication:
- March 2022
-
- Article
- Export citation
CUTOFF AT THE ENTROPIC TIME FOR RANDOM WALKS ON COVERED EXPANDER GRAPHS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1571-1616
- Print publication:
- September 2022
-
- Article
- Export citation
AN ANALOGUE OF HUPPERT’S CONJECTURE FOR CHARACTER CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 278-286
- Print publication:
- October 2021
-
- Article
- Export citation
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
- Print publication:
- September 2021
-
- Article
- Export citation
A variant of the Corners theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 607-621
- Print publication:
- November 2021
-
- Article
- Export citation
CORES OVER RAMSEY STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 352-361
- Print publication:
- March 2021
-
- Article
- Export citation
THE OPEN AND CLOPEN RAMSEY THEOREMS IN THE WEIHRAUCH LATTICE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 316-351
- Print publication:
- March 2021
-
- Article
- Export citation
On the Erdős–Sós conjecture for trees with bounded degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 741-761
-
- Article
- Export citation
The number of maximum primitive sets of integers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 781-795
-
- Article
- Export citation
A structure theorem for stochastic processes indexed by the discrete hypercube
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e8
-
- Article
-
- You have access
- Open access
- Export citation
Moves on k-graphs preserving Morita equivalence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 28 January 2021, pp. 655-685
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation