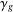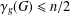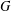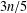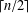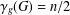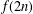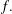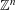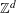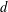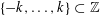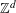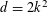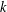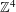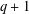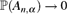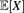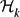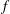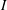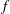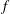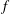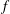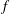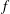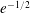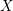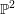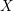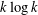Refine listing
Actions for selected content:
1718 results in 05xxx
Multiple Lattice Tilings in Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 923-929
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
THE DOMINATION GAME ON SPLIT GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 327-337
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
PARITY RESULTS FOR PARTITIONS WHEREIN EACH PART APPEARS AN ODD NUMBER OF TIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 51-55
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
A Combinatorial Approach to Small Ball Inequalities for Sums and Differences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 November 2018, pp. 100-129
-
- Article
- Export citation
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
- Export citation
Sparse Highly Connected Spanning Subgraphs in Dense Directed Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 05 November 2018, pp. 423-464
-
- Article
- Export citation
Polynomial Mixing of the Edge-Flip Markov Chain for Unbiased Dyadic Tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 365-387
-
- Article
- Export citation
TILING WITH PUNCTURED INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-189
- Print publication:
- 2019
-
- Article
- Export citation
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Parking on a Random Tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 23-45
-
- Article
- Export citation
On Erdős–Ko–Rado for Random Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 October 2018, pp. 61-80
-
- Article
- Export citation
Amenability and unique ergodicity of automorphism groups of countable homogeneous directed graphs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1351-1401
- Print publication:
- May 2020
-
- Article
- Export citation
Newton Complementary Duals of
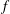 $f$-Ideals
$f$-Ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 231-241
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Local Convergence and Stability of Tight Bridge-addable Classes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 15 October 2018, pp. 563-601
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
THE FRIENDSHIP PARADOX FOR WEIGHTED AND DIRECTED NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 136-145
-
- Article
- Export citation
Foundations of Boij–Söderberg theory for Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 11 September 2018, pp. 2205-2238
- Print publication:
- October 2018
-
- Article
- Export citation
Line arrangements and configurations of points with an unexpected geometric property
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 2150-2194
- Print publication:
- October 2018
-
- Article
- Export citation
COLORING CURVES ON SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 04 September 2018, e17
-
- Article
-
- You have access
- Open access
- Export citation
From trees to graphs: collapsing continuous-time branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 900-919
- Print publication:
- September 2018
-
- Article
- Export citation
Disparity of clustering coefficients in the Holme‒Kim network model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 918-943
- Print publication:
- September 2018
-
- Article
- Export citation