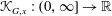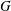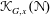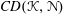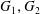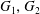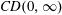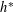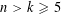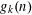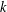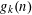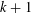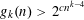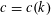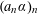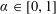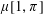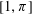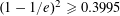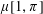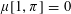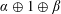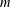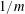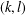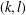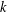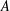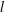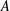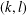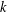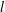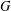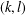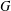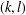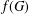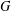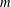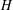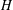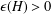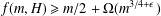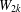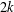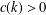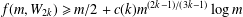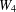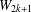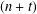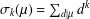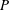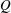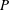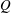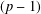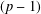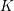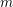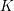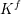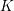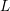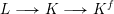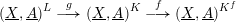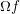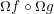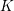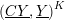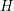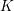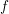Refine listing
Actions for selected content:
1718 results in 05xxx
Bakry–Émery Curvature Functions on Graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 89-143
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
PBW Bases and Marginally Large Tableaux in Types B and C
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 37-54
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
THE ERDŐS–SZEKERES PROBLEM AND AN INDUCED RAMSEY QUESTION
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 702-707
- Print publication:
- 2019
-
- Article
- Export citation
HADAMARD MATRICES AND 1-FACTORIZATIONS OF COMPLETE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 488-499
- Print publication:
- 2019
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
- Print publication:
- 2019
-
- Article
- Export citation
ZEROS OF THE MÖBIUS FUNCTION OF PERMUTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1074-1092
- Print publication:
- 2019
-
- Article
- Export citation
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
A problem of integer partitions and numerical semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 969-978
- Print publication:
- August 2019
-
- Article
- Export citation
THE MAXIMUM SIZE OF
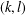 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
MAXIMUM CUTS IN GRAPHS WITHOUT WHEELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 13-26
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 353-361
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Diameter, Decomposability, and Minkowski Sums of Polytopes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 741-755
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
An Upper Bound on the Size of Avoidance Couplings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 325-334
-
- Article
- Export citation
Random systems in ultrametric spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 83-97
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
The degree-wise effect of a second step for a random walk on a graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1203-1210
- Print publication:
- December 2018
-
- Article
- Export citation
Preferential attachment graphs with co-existing types of different fitnesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1211-1227
- Print publication:
- December 2018
-
- Article
- Export citation
Almost Gentle Algebras and their Trivial Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 489-504
-
- Article
- Export citation
CONGRUENCES FOR THE
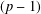 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
The homotopy theory of polyhedral products associated with flag complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 206-228
- Print publication:
- January 2019
-
- Article
- Export citation