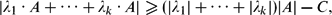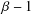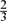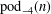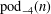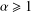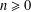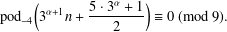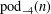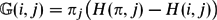Refine listing
Actions for selected content:
1718 results in 05xxx
On the Number of Bh-Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 16 September 2015, pp. 108-129
-
- Article
- Export citation
Sum of Many Dilates
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 08 September 2015, pp. 460-469
-
- Article
- Export citation
Distance between two random k-out digraphs, with and without preferential attachment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 858-879
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A FORMULA FOR THE NUMBER OF SPANNING TREES IN CIRCULANT GRAPHS WITH NONFIXED GENERATORS AND DISCRETE TORI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 25 August 2015, pp. 365-373
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A REMARK ON TAIL DISTRIBUTIONS OF PARTITION RANK AND CRANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 20 August 2015, pp. 31-36
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
A Stability Result for the Union-Closed Size Problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 18 August 2015, pp. 399-418
-
- Article
- Export citation
Simple Containers for Simple Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 17 August 2015, pp. 448-459
-
- Article
- Export citation
ON ISOMORPHISMS OF VERTEX-TRANSITIVE CUBIC GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 13 August 2015, pp. 341-349
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The Satisfiability Threshold for k-XORSAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 31 July 2015, pp. 236-268
-
- Article
- Export citation
Universality of Graphs with Few Triangles and Anti-Triangles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 29 July 2015, pp. 560-576
-
- Article
- Export citation
DUAL EQUIVALENCE GRAPHS I: A NEW PARADIGM FOR SCHUR POSITIVITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 22 July 2015, e12
-
- Article
-
- You have access
- Open access
- Export citation
EXPLICIT CONSTRUCTION OF COMPANION BASES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 357-384
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
JACK–LAURENT SYMMETRIC FUNCTIONS FOR SPECIAL VALUES OF PARAMETERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 599-616
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ISOMORPHIC INDUCED MODULES AND DYNKIN DIAGRAM AUTOMORPHISMS OF SEMISIMPLE LIE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 187-203
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
An Improvement of the Beck–Fiala Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 06 July 2015, pp. 380-398
-
- Article
- Export citation
On the “Preconditioning” Function Used in Planewave DFT Calculations and its Generalization
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 167-179
- Print publication:
- July 2015
-
- Article
- Export citation
A Hitting Time Formula for the Discrete Green's Function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 29 June 2015, pp. 362-379
-
- Article
- Export citation
The Interpolation Method for Random Graphs with Prescribed Degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 19 June 2015, pp. 436-447
-
- Article
- Export citation
STABILITY PATTERNS IN REPRESENTATION THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e11
-
- Article
-
- You have access
- Open access
- Export citation