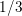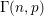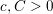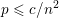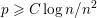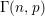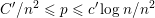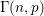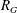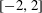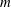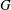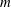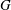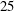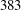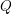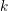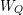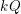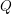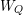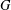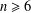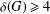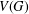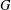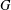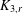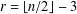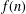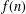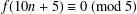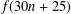Refine listing
Actions for selected content:
1765 results in 05xxx
ON CONFIGURATIONS WHERE THE LOOMIS–WHITNEY INEQUALITY IS NEARLY SHARP AND APPLICATIONS TO THE FURSTENBERG SET PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 145-161
- Print publication:
- January 2015
-
- Article
- Export citation
Decomposing Random Graphs into Few Cycles and Edges
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 December 2014, pp. 857-872
-
- Article
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
-
- Article
-
- You have access
- Export citation
A Short Proof of the Random Ramsey Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 22 December 2014, pp. 130-144
-
- Article
- Export citation
Minimum Number of Monotone Subsequences of Length 4 in Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 19 December 2014, pp. 658-679
-
- Article
- Export citation
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
The front of the epidemic spread and first passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 101-121
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
How Clustering Affects Epidemics in Random Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 985-1008
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Continuum AB percolation and AB random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 333-344
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Asymptotic hitting probabilities for the Bolthausen-Sznitman coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 87-97
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Percolation on the Information-Theoretically Secure Signal to Interference Ratio Graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 910-920
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The probability that a random multigraph is simple. II
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 123-137
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Random triangular groups at density
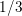 $1/3$
$1/3$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 167-178
- Print publication:
- January 2015
-
- Article
- Export citation
EXPANSION CONSTANTS AND HYPERBOLIC EMBEDDINGS OF FINITE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 1-13
- Print publication:
- January 2015
-
- Article
- Export citation
A classification of all 1-Salem graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 November 2014, pp. 582-594
-
- Article
-
- You have access
- Export citation
ROW CONVEX TABLEAUX AND BOTT–SAMELSON VARIETIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 23 October 2014, pp. 315-330
-
- Article
-
- You have access
- Export citation
Quotient closed subcategories of quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
- Print publication:
- March 2015
-
- Article
- Export citation
A NOTE ON ALMOST BALANCED BIPARTITIONS OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 177-182
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ESTIMATION AND COMPUTATION WITH MATRICES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 175-176
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 41-46
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
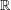
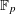
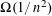
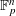
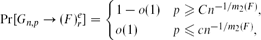
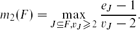
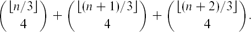
 the probability that the multigraph is simple stays away from 0 if and only if
the probability that the multigraph is simple stays away from 0 if and only if 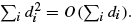 The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.
The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.