Refine listing
Actions for selected content:
1718 results in 05xxx
Birth of a Strongly Connected Giant in an Inhomogeneous Random Digraph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 601-611
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Galois groups of chromatic polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 281-307
-
- Article
-
- You have access
- Export citation
Distribution of Minimal Path Lengths when Edge Lengths are Independent Heterogeneous Exponential Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 895-900
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Coagulation Processes with Gibbsian Time Evolution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 612-626
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
The Class of Tenable Zero-Balanced Pólya Urn Schemes: Characterization and Gaussian Phases
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 702-728
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
BIPARTITE DIVISOR GRAPH FOR THE PRODUCT OF SUBSETS OF INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 288-297
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
ON A STRONG VERSION OF THE KEPLER CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 August 2012, pp. 23-30
- Print publication:
- January 2013
-
- Article
-
- You have access
- Export citation
Quivers of monoids with basic algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1516-1560
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
DEGREE DISTANCE AND MINIMUM DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 09 July 2012, pp. 255-271
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
On Tail Bounds for Random Recursive Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 566-581
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Typical Distances in Ultrasmall Random Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 583-601
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
On the Joint Behavior of Types of Coupons in Generalized Coupon Collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 429-451
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
FINITE REGULAR BANDS ARE FINITELY RELATED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1-9
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Groups acting simply transitively on vertex sets of hyperbolic triangular buildings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 101-112
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC ENUMERATION OF SYMMETRIC INTEGER MATRICES WITH UNIFORM ROW SUMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 March 2012, pp. 367-384
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Percolation and Connectivity in AB Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 21-41
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
An Sir Epidemic Model on a Population with Random Network and Household Structure, and Several Types of Individuals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 63-86
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Joint Vertex Degrees in the Inhomogeneous Random Graph Model ℊ(n,{pij })
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 139-165
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
RAMSEY NUMBERS FOR TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 164-176
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
A MINIMUM DEGREE CONDITION FOR FRACTIONAL ID-[a,b]-FACTOR-CRITICAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 177-183
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
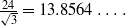
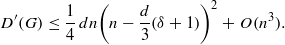
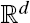 , the
, the 