Refine listing
Actions for selected content:
1765 results in 05xxx
Gaussian phases in generalized coupon collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 994-1012
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
NONEXISTENCE OF A CIRCULANT EXPANDER FAMILY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 87-95
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
ON A COMBINATORIAL PROOF FOR AN IDENTITY INVOLVING THE TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 46-49
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Criticality of the exponential rate of decay for the largest nearest-neighbor link in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 631-658
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Extreme value theory, Poisson-Dirichlet distributions, and first passage percolation on random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 706-738
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Phases in the Diffusion of Gases via the Ehrenfest URN Modelx
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 841-855
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Poisson Approximation of the Number of Cliques in Random Intersection Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 826-840
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Gibbs Random Fields with Unbounded Spins on Unbounded Degree Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-875
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Limit theorems for random spatial drainage networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 659-688
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
RESIDUAL PROPERTIES OF SIMPLE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 August 2010, pp. 488-504
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON DEFINING SETS IN LATIN SQUARES AND TWO INTERSECTION PROBLEMS, ONE FOR LATIN SQUARES AND ONE FOR STEINER TRIPLE SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 351-352
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
The minimal density of triangles in tripartite graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 388-413
-
- Article
-
- You have access
- Export citation
SEMIREGULAR FACTORIZATIONS OF REGULAR MULTIGRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 13 July 2010, pp. 357-362
- Print publication:
- July 2010
-
- Article
- Export citation
ON THE NUMBER OF LATIN RECTANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 167-170
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
SOLUTION TO A QUESTION ON A FAMILY OF IMPRIMITIVE SYMMETRIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 79-83
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Preferential duplication graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 572-585
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Degree sequences of geometric preferential attachment graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 319-330
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Random subgraph counts and U-statistics: multivariate normal approximation via exchangeable pairs and embedding
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 378-393
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Towards a combinatorial representation theory for the rational Cherednik algebra of type G(r, p, n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 419-445
-
- Article
-
- You have access
- Export citation
From permutahedron to associahedron
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 299-310
-
- Article
-
- You have access
- Export citation
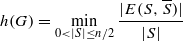
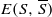 denotes the set of edges in
denotes the set of edges in 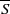 . An expander family is a sequence {
. An expander family is a sequence {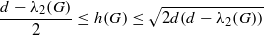
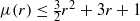 if
if 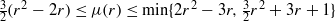 if
if 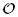 for the rational Cherednik algebra of type
for the rational Cherednik algebra of type 