Refine listing
Actions for selected content:
1718 results in 05xxx
On the distribution of distances in recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 749-757
- Print publication:
- September 1996
-
- Article
- Export citation
Decomposing cubes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-128
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
The random division of faces in a planar graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 377-383
- Print publication:
- June 1996
-
- Article
- Export citation
Multivariate normal approximations by Stein's method and size bias couplings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-17
- Print publication:
- March 1996
-
- Article
- Export citation
Asymptotic properties of rooted 3-connected maps on surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-41
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
A generalization of Evans' Theorem: embedding partial tricycle systems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-408
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Constructions for arc-transitive digraphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-80
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
The number of trees with large diameter
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 298-311
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
Balanced directed cycle designs based on cyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 210-218
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Renewal-type behavior of absorption times in Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 988-1005
- Print publication:
- December 1994
-
- Article
- Export citation
A note on the union-closed sets conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-236
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Regular maps with small parameters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-112
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation
Constructing graphs which are ½-transitive
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-402
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
A regular endomorphism of a graph and its inverses
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-198
- Print publication:
- June 1994
-
- Article
- Export citation
On the clique number of a random overlap graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 582-588
- Print publication:
- June 1994
-
- Article
- Export citation
The Falling-Leaves Mosaic and its Equilibrium Properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 54-62
- Print publication:
- March 1994
-
- Article
- Export citation
How to obtain an asymptotic expansion of a sequence from an analytic identity satisfied by its generating function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-143
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Vertex-transitive graphs which are not Cayley graphs, I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-63
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Transient analysis of M/M/1 queues in discrete time by general server vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-129
- Print publication:
- 1994
-
- Article
- Export citation
A note of the union-closed sets conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-413
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
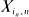 is asymptotically normal in several settings.
is asymptotically normal in several settings.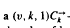 -design, is a decomposition of the complete directed graph
-design, is a decomposition of the complete directed graph 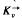 into edge disjoint directed cycles of length
into edge disjoint directed cycles of length 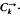 -designs admitting the holomorph {ø
-designs admitting the holomorph {ø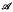 there exists some element which is contained in at least half the sets in
there exists some element which is contained in at least half the sets in 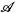 = {A
= {A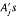 .
.