Refine listing
Actions for selected content:
1718 results in 05xxx
Balanced tournament designs with almost orthogonal resolutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-195
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
On the average number of real zeros of a class of random algebraic equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-160
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Constructions of balanced ternary designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 320-332
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Graphs which are vertex-critical with respect to the edge-chromatic class
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-252
- Print publication:
- December 1989
-
- Article
- Export citation
Total chromatic number of graphs of high degree
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 445-452
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
On the zeroes of profiles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 424-429
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
Graphs associated with triangulations of lattice polygons
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-398
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
Bijective Proofs of Some n-Color Partition Identities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-332
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Une Note sur les Coefficients Binomiaux de Gauss
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-343
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A new proof of the Doyen-Wilson theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 32-42
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Major n-connected graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-52
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
An infinite class of Hadamard matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-394
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
Some new series of Hadamard matrices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-383
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
An algorithm for the ear decomposition of a 1-factor covered graph
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 296-301
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Maximal-clique partitions of interval graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-232
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
Primitive permutation groups with a doubly transitive subconstituent
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-77
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Note on the vertex 2–connectivity of a graph
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 1 / June 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-71
- Print publication:
- June 1988
-
- Article
- Export citation
A note on group divisible designs with mutually orthogonal resolutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 397-401
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
Isomorphic factorization of regular graphs of even degree
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 3 / June 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 402-420
- Print publication:
- June 1988
-
- Article
-
- You have access
- Export citation
The existence of a class of Kirkman squares of index 2
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-41
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation
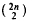 ) distinct unordered pairs of the elements of
) distinct unordered pairs of the elements of 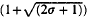 log
log 