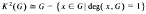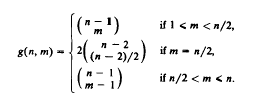Refine listing
Actions for selected content:
1713 results in 05xxx
Matroids whose ground sets are domains of functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 380-387
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Doubly regular tournaments of Szekeres type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-404
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
A result on iterated clique graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-294
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Quasi Clifford algebras and systems of orthogonal designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 1 / January 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-23
- Print publication:
- January 1982
-
- Article
-
- You have access
- Export citation
A generalization of Sperner's theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-485
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Terminal path numbers for certain families of trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-438
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
The spectrum of skew Room squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 475-480
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Some results concerning frames, Room squares, and subsquares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 376-384
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
The Hadamard conjecture and circuits of length four in a complete bipartite graph
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 252-256
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
An extremal problem in hypergraph theory (II)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-135
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
Another class of graceful trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 226-235
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
On the ranks of some (0, 1)-matrices with constant row sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 2 / August 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-201
- Print publication:
- August 1981
-
- Article
-
- You have access
- Export citation
On ordered set systems and some conjectures related to the erdös–ko–rado theorem and turán's theorem
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 54-66
- Print publication:
- June 1981
-
- Article
- Export citation
Ramsey numbers for certain k-graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 284-296
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Integral quadratic forms and orthogonal designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-306
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
On the reconstruction conjecture for separable graphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-320
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Relations, homogeneity and group quotients
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-355
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Random labelled trees and their branching networks
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-237
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Linear spaces with line range {n−1, n, n + 1} and at most n2 points
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 215-228
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Nonexistence of an extremal graph of a certain type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-64
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
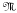 of matroids so obtained is closed under restriction, contraction, duality, truncation and elongation, but not under direct sum. We give an excluded-minor characterization of
of matroids so obtained is closed under restriction, contraction, duality, truncation and elongation, but not under direct sum. We give an excluded-minor characterization of