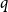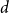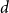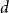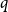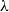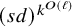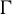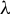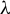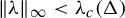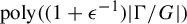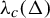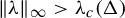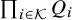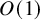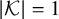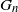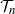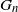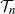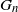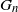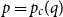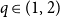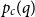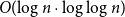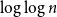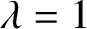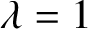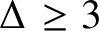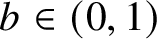Refine listing
Actions for selected content:
85 results in 68Wxx
Strong discrete Morse theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central limit theorems for additive functionals of patricia tries
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-14
-
- Article
- Export citation
Glauber dynamics for the hard-core model on bounded-degree
 $H$-free graphs
$H$-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 803-814
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE PRIMITIVITY OF THE TRINOMIAL
 $x^{n}+ax^{k}+b$ OVER
$x^{n}+ax^{k}+b$ OVER  $\mathbb {F}_{q}$
$\mathbb {F}_{q}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-5
-
- Article
- Export citation
Convergence of the QuickVal residual
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 780-802
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two relaxed inertial forward-backward-forward algorithms for solving monotone inclusions and an application to compressed sensing
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-22
-
- Article
- Export citation
Sampling repulsive Gibbs point processes using random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact recovery of community detection in k-community Gaussian mixture models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 491-523
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 487-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis of
 ${\textit{d}}$-ary tree algorithms with successive interference cancellation
${\textit{d}}$-ary tree algorithms with successive interference cancellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1075-1105
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasipolynomial-time algorithms for Gibbs point processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficient simplicial replacement of semialgebraic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate and discrete Euclidean vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 March 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial Euler operators and the efficient inversion of Div
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1046-1066
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An efficient method for generating a discrete uniform distribution using a biased random source
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 1069-1078
- Print publication:
- September 2023
-
- Article
- Export citation
A generalized Sylvester–Gallai-type theorem for quadratic polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surprising identities for the greedy independent set on Cayley trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2022, pp. 1042-1058
- Print publication:
- December 2022
-
- Article
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lee–Yang zeros and the complexity of the ferromagnetic Ising model on bounded-degree graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation