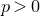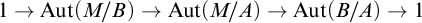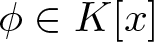Refine listing
Actions for selected content:
205 results in 12xxx
AN EFFECTIVE VERSION OF THE PRIMITIVE ELEMENT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-8
-
- Article
- Export citation
Improvements on dimension growth results and effective Hilbert’s irreducibility theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic versions of mass formulas by Krasner, Serre and Bhargava
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 826-832
- Print publication:
- December 2025
-
- Article
- Export citation
ON THE PRIMITIVITY OF THE TRINOMIAL
 $x^{n}+ax^{k}+b$ OVER
$x^{n}+ax^{k}+b$ OVER  $\mathbb {F}_{q}$
$\mathbb {F}_{q}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-5
-
- Article
- Export citation
Universal-existential theories of fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-30
-
- Article
- Export citation
Infinite matroids in tropical differential algebra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semisimple groups interpretable in various valued fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 August 2025, e127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising local fields of positive characteristic by Galois theory and the Brauer group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 2136-2153
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTING ENDOMORPHISMS OF VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 2047-2106
- Print publication:
- September 2025
-
- Article
- Export citation
KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF DIFFERENTIAL-HENSELIAN PRE-H-FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-formality of Galois cohomology modulo all primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 12 August 2025, pp. 831-858
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE TRANSCENDENCE DEGREE OF THE REALS OVER CERTAIN SET-THEORETICAL SUBFIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-18
-
- Article
- Export citation
A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 52-67
- Print publication:
- March 2025
-
- Article
- Export citation
ARITHMETIC-GEOMETRIC MEAN SEQUENCES OVER FINITE FIELDS
 $\mathbb {F}_q$, WHERE
$\mathbb {F}_q$, WHERE  $q\equiv 5$ (mod 8)
$q\equiv 5$ (mod 8)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 473-484
- Print publication:
- December 2025
-
- Article
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 458-472
- Print publication:
- December 2025
-
- Article
- Export citation
THE SHORT EXACT SEQUENCE IN DEFINABLE GALOIS COHOMOLOGY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 30 January 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irreducible factors of a polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 573-582
-
- Article
- Export citation
UPPER BOUNDS ON POLYNOMIAL ROOT SEPARATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 274-289
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation






























 . If
. If