Refine listing
Actions for selected content:
57 results in 46Jxx
Invariant subspaces in the bidisc and commutators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-242
-
- Article
-
- You have access
- Export citation
Relative amenability and the non-amenability of B(l1)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-333
-
- Article
-
- You have access
- Export citation
Extremal problems in Hp
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-110
-
- Article
-
- You have access
- Export citation
Ergodicity and stability of orbits of unbounded semigroup representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-232
-
- Article
-
- You have access
- Export citation
The second dual of C0 (S, A)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-313
-
- Article
-
- You have access
- Export citation
Interpolation problem for l1 and a uniform algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
Two commutative amenable non-symmetric Banach algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-231
-
- Article
-
- You have access
- Export citation
Uniform spaces, spanier quasitopologies, and a duality for locally convex algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 99-128
-
- Article
-
- You have access
- Export citation
Homomorphisms of the algebra of locally integrable functions on the half line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-278
-
- Article
-
- You have access
- Export citation
Ideals in the Wiener algebra W+
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-228
-
- Article
-
- You have access
- Export citation
Harmonic analysis on the Fourier algebras A1, p(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-452
-
- Article
-
- You have access
- Export citation
Amenability and ideals in A(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-155
-
- Article
-
- You have access
- Export citation
Generalized hypergroups and orthogonal polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-394
-
- Article
-
- You have access
- Export citation
Some Inequalities arising from a Banach algebra norm
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-202
-
- Article
-
- You have access
- Export citation
On unilateral shift operators and C0-operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-142
-
- Article
-
- You have access
- Export citation
UNIFORM APPROXIMATION BY POLYNOMIAL, RATIONAL AND ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 387-399
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
INVARIANT SUBSPACES IN THE BIDISC AND WANDERING SUBSPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 367-374
-
- Article
-
- You have access
- Export citation
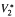 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.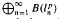 is no amenable for 1 ≤
is no amenable for 1 ≤ 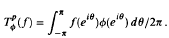
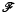 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 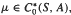 ,
, 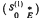 relative to a decomposition ℳ ⊕
relative to a decomposition ℳ ⊕ 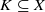 . Let
. Let 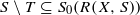 and
and 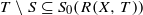 ;
;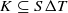 ;
;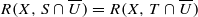 for every open set
for every open set 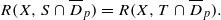
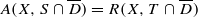 for every closed disk
for every closed disk 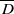 in ℂ ;
in ℂ ;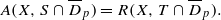
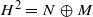 . Using the wandering subspace of
. Using the wandering subspace of 