Refine listing
Actions for selected content:
433 results in 46Lxx
Crossed products of Hilbert C*-bimodules by bundles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-135
-
- Article
-
- You have access
- Export citation
Some groups with T1 primitive ideal spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-64
-
- Article
-
- You have access
- Export citation
On the convergence of a sequence of completely positive maps to the identity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 340-348
-
- Article
-
- You have access
- Export citation
Partial automorphisms of stable C*-algebras and Hilbert C*-bimodules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-398
-
- Article
-
- You have access
- Export citation
CONTINUOUS AND DISCRETE FLOWS ON OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 169-176
-
- Article
-
- You have access
- Export citation
A KADISON–SAKAI-TYPE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 249-257
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Amalgamated free products of C*-bundles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 23-36
-
- Article
-
- You have access
- Export citation
Hecke C*-algebras and semi-direct products
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 127-153
-
- Article
-
- You have access
- Export citation
Morita equivalences and KK-theory for Banach algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 565-593
- Print publication:
- July 2009
-
- Article
- Export citation
A MEAN ERGODIC THEOREM FOR ACTIONS OF AMENABLE QUANTUM GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 87-95
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
AMENABILITY FOR REAL C*-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 509-514
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
LOCAL PROPERTIES OF THE HOCHSCHILD COHOMOLOGY OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 117-130
-
- Article
-
- You have access
- Export citation
THE K-THEORY OF SOME HIGHER RANK EXEL–LACA ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-38
-
- Article
-
- You have access
- Export citation
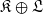 and
and 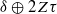 , where
, where 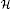 when
when 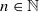 , bounded local
, bounded local 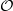 be a higher rank Exel–Laca algebra generated by an alphabet
be a higher rank Exel–Laca algebra generated by an alphabet 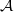 . If
. If 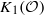 is trivial and
is trivial and  is isomorphic to
is isomorphic to 