Refine listing
Actions for selected content:
51 results in 54Fxx
Periodic points for amenable group actions on uniquely arcwise connected continua
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 30 September 2020, pp. 2833-2844
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
DIMENSION INEQUALITY FOR A DEFINABLY COMPLETE UNIFORMLY LOCALLY O-MINIMAL STRUCTURE OF THE SECOND KIND
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1654-1663
- Print publication:
- December 2020
-
- Article
- Export citation
On cohesive almost zero-dimensional spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 July 2020, pp. 429-441
- Print publication:
- June 2021
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
- Print publication:
- June 2020
-
- Article
- Export citation
EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 20 August 2019, pp. 311-324
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
EMBEDDING OF THE FREE ABELIAN TOPOLOGICAL GROUP
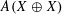 $A(X\oplus X)$ INTO
$A(X\oplus X)$ INTO 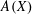 $A(X)$
$A(X)$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 708-718
- Print publication:
- 2019
-
- Article
- Export citation
ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS
 $4$
$4$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 May 2017, pp. 673-706
- Print publication:
- July 2019
-
- Article
- Export citation
LINEAR SURJECTIVE ISOMETRIES BETWEEN VECTOR-VALUED FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 349-373
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
COARSE AMENABILITY AND DISCRETENESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 21 October 2015, pp. 65-77
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
CHAINS OF FUNCTIONS IN
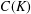 $C(K)$-SPACES
$C(K)$-SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 350-363
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A RESULT ON MONOTONICALLY LINDELÖF GENERALIZED ORDERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 18 August 2011, pp. 481-483
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON PARACOMPACT p-SPACES AND THE MONOTONE D-PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 463-469
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
MONOTONE LINDELÖF PROPERTY AND LINEARLY ORDERED EXTENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 418-424
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Mutually Aposyndetic Decomposition of Homogeneous Continua: Dedicated to Charles L. Hagopian and James T. Rogers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-201
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON CONTINUOUSLY URYSOHN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 472-475
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On Banach-Mazur compacta
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 316-335
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
The Nachibin quasi-uniformity of a bi-Stonian space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-326
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
The Urysohn-Menger sum formula: an extension of the Dydak-Walsh theorem to dimension one
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-282
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Strongly zero-dimensional bispaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 3 / December 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-337
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Euclidean representations of topologically ordered spaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-135
- Print publication:
- June 1992
-
- Article
- Export citation
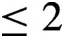
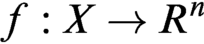
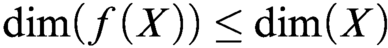
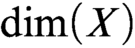
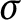
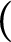
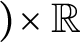
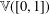
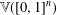
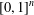
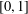

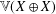
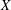
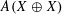
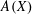
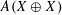
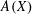
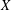

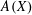
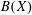

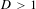
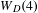
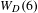
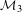
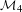
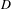
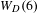

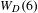

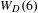
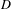
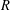
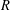
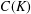
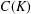
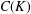
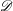
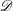
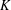
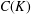
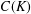
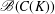
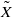 be the minimal dense linearly ordered extension of
be the minimal dense linearly ordered extension of 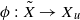 , ϕ(〈
, ϕ(〈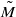 is a paracompact
is a paracompact 