Refine listing
Actions for selected content:
351 results in 20Exx
On the depth of subgroups of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 14 / 2026
- Published online by Cambridge University Press:
- 20 February 2026, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WEIGHT CONJECTURES FOR FUSION SYSTEMS ON AN EXTRASPECIAL GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 February 2026, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH ONLY NEARLY NORMAL OR CONTRANORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-10
-
- Article
- Export citation
Liminal
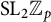 $\mathrm {SL}_2 \mathbb{Z}_{p}$-representations and odd-th cyclic covers of genus one two-bridge knots
$\mathrm {SL}_2 \mathbb{Z}_{p}$-representations and odd-th cyclic covers of genus one two-bridge knots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 23 January 2026, pp. 1-11
-
- Article
- Export citation
THE REIDEMEISTER SPECTRUM OF ZM-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-6
-
- Article
- Export citation
Wreath products and the non-coprime k(GV) problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTION OF COMMUTATOR BLUEPRINTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 120 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DYNAMICS OF ENDOMORPHISMS OF THE DIRECT PRODUCT OF TWO FREE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 120 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 17 October 2025, pp. 34-56
-
- Article
- Export citation
A note on morphisms to wreath products
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 08 October 2025, pp. 247-274
- Print publication:
- March 2026
-
- Article
- Export citation
The conjugacy ratio of abelian-by-cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 69 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 17 September 2025, pp. 339-362
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On integral decomposition of unipotent elements in integral group rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Rokhlin property for mapping class groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 69 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 02 September 2025, pp. 37-59
-
- Article
- Export citation
Type invariants for non-abelian odometers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 01 September 2025, pp. 182-210
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On finite groups with bounded conjugacy classes of commutators
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-6
-
- Article
- Export citation
On congruence subgroups generated by two parabolic rational matrices
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 15-34
- Print publication:
- January 2026
-
- Article
- Export citation
On closure operations in the space of subgroups and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 05 August 2025, pp. 3728-3748
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the quasi-transitivity degree of branch groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 04 August 2025, pp. 695-715
- Print publication:
- November 2025
-
- Article
- Export citation
GROUPS WITH DENSE TRANSITIVELY NORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-7
-
- Article
- Export citation
On derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation