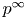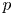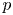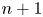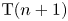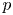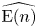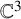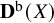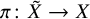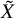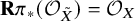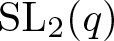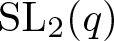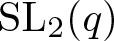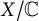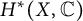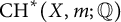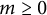Refine listing
Actions for selected content:
181 results in 19xxx
Tachikawa's second conjecture, derived recollements, and gendo-symmetric algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2704-2737
- Print publication:
- November 2024
-
- Article
- Export citation
Eisenstein cocycles in motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 30 October 2024, pp. 2407-2479
- Print publication:
- October 2024
-
- Article
- Export citation
A NONCOMMUTATIVE ANALOGUE OF CLAUSEN’S VIEW ON THE IDÈLE CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2777-2824
- Print publication:
- November 2024
-
- Article
- Export citation
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Boundedness of the p-primary torsion of the Brauer group of an abelian variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 463-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CATEGORICAL APPROACH TO THE BAUM–CONNES CONJECTURE FOR ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 2319-2364
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher semiadditive algebraic K-theory and redshift
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 237-287
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categorical and K-theoretic Donaldson–Thomas theory of
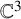 $\mathbb {C}^3$ (part II)
$\mathbb {C}^3$ (part II)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 December 2023, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On distributivity in higher algebra I: the universal property of bispans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2326-2415
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homological Bondal-Orlov localization conjecture for rational singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The localisation theorem for the K-theory of stable ∞-categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 July 2023, pp. 1749-1785
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trivial source character tables of
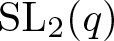 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 689-709
-
- Article
- Export citation
REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1461-1518
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISATIONS OF LODAY’S ASSEMBLY MAPS FOR LAWVERE’S ALGEBRAIC THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 811-837
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-THEORY OF NON-ARCHIMEDEAN RINGS II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 21 February 2023, pp. 669-685
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECIAL VALUES OF ZETA-FUNCTIONS OF REGULAR SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 December 2022, pp. 495-519
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enough vector bundles on orbispaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 28 November 2022, pp. 2046-2081
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bökstedt periodicity and quotients of DVRs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1683-1712
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The complexity of higher Chow groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 29 July 2022, pp. 903-911
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation