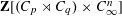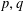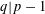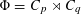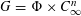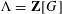Refine listing
Actions for selected content:
181 results in 19xxx
A FUNCTIONAL LOGARITHMIC FORMULA FOR THE HYPERGEOMETRIC FUNCTION
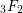 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 29-46
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS
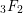 $_{3}F_{2}$
$_{3}F_{2}$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2018, pp. 47-62
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Poitou–Tate duality for arithmetic schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 23 August 2018, pp. 2020-2044
- Print publication:
- September 2018
-
- Article
- Export citation
Excision in algebraic
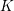 $K$-theory revisited
$K$-theory revisited
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1801-1814
- Print publication:
- September 2018
-
- Article
- Export citation
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
- Print publication:
- May 2020
-
- Article
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
Rational Cup Product and Algebraic K0-Groups of Rings of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 607-622
-
- Article
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
Segal's Spectral Sequence in Twisted Equivariant K-theory for Proper and Discrete Actions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 121-150
-
- Article
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
- Print publication:
- January 2020
-
- Article
- Export citation
Zero cycles with modulus and zero cycles on singular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 120-187
- Print publication:
- January 2018
-
- Article
- Export citation
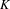 $K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
$K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 10 August 2017, pp. 1051-1085
- Print publication:
- September 2019
-
- Article
- Export citation
VANISHING OF THE NEGATIVE HOMOTOPY
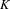 $K$-THEORY OF QUOTIENT SINGULARITIES
$K$-THEORY OF QUOTIENT SINGULARITIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 08 May 2017, pp. 619-627
- Print publication:
- May 2019
-
- Article
- Export citation
Régulateurs modulaires explicites via la méthode de Rogers–Zudilin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1119-1152
- Print publication:
- June 2017
-
- Article
- Export citation
On higher regulators of Siegel threefolds II: the connection to the special value
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 889-946
- Print publication:
- May 2017
-
- Article
- Export citation
A REMARK ON THE STABLE REAL FORMS OF COMPLEX VECTOR BUNDLES OVER MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 69-76
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Coarse flow spaces for relatively hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 09 March 2017, pp. 745-779
- Print publication:
- April 2017
-
- Article
- Export citation
Rings of Polynomials With Artinian Coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 947-954
-
- Article
- Export citation
STABLY FREE MODULES OVER
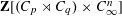 $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 22 February 2017, pp. 451-461
- Print publication:
- 2017
-
- Article
- Export citation
An approach to intersection theory on singular varieties using motivic complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2371-2404
- Print publication:
- November 2016
-
- Article
- Export citation
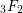
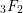
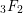

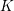
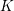
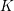
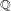
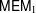
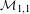

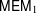

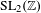
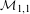
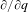
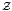 ) in terms of Cu(
) in terms of Cu(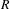
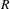
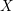
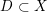

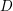
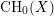
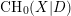
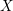

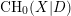
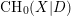
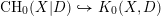
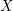
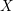
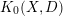
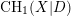
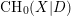
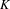
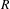
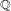
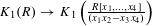
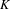
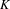
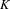
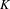
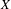
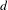
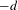
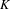
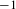
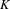
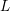
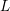
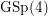

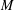

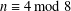
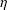
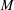
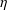
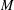
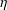
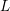
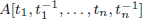 with coefficients in an Artinian ring
with coefficients in an Artinian ring