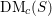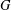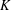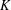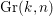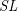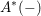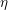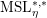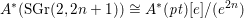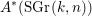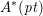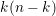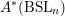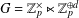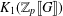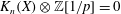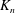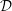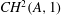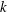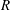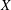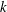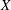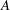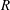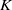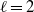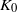Refine listing
Actions for selected content:
181 results in 19xxx
Projective geometry in characteristic one and the epicyclic category
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-132
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Classifying Polygonal Algebras by their K0-Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 13 February 2015, pp. 485-497
-
- Article
-
- You have access
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
THE GROMOV-LAWSON-ROSENBERG CONJECTURE FOR THE SEMI-DIHEDRAL GROUP OF ORDER 16
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 365-386
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
ON DIFFERENTIAL CHARACTERISTIC CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 30-47
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
PRO CDH-DESCENT FOR CYCLIC HOMOLOGY AND
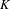 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 539-567
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
ÉTALE MOTIVIC COHOMOLOGY AND ALGEBRAIC CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 24 November 2014, pp. 511-537
- Print publication:
- July 2016
-
- Article
- Export citation
The special linear version of the projective bundle theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 461-501
- Print publication:
- March 2015
-
- Article
- Export citation
HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL
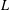 $L$-VALUES
$L$-VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 1-38
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
KAROUBI’S RELATIVE CHERN CHARACTER, THE RIGID SYNTOMIC REGULATOR, AND THE BLOCH–KATO EXPONENTIAL MAP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 20 August 2014, e20
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing of negative
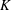 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1425-1434
- Print publication:
- August 2014
-
- Article
- Export citation
The elliptic Weyl character formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 1196-1234
- Print publication:
- July 2014
-
- Article
- Export citation
Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-
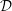 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 691-711
- Print publication:
- April 2014
-
- Article
- Export citation
Noncommutative motives of Azumaya algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 March 2014, pp. 379-403
- Print publication:
- April 2015
-
- Article
- Export citation
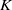 $K$ -theory of one-dimensional rings via pro-excision
$K$ -theory of one-dimensional rings via pro-excision
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 23 July 2013, pp. 225-272
- Print publication:
- April 2014
-
- Article
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation
QUASI MULTIPLICATION AND
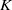 $K$-GROUPS
$K$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 257-267
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
On primordial groups for the Green ring
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 337-347
-
- Article
-
- You have access
- Export citation
Kontsevich’s noncommutative numerical motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 12 October 2012, pp. 1811-1820
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation

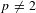
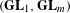
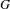
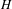

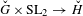
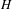
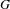
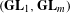
 of the identity in
of the identity in