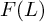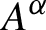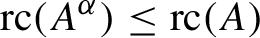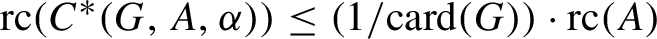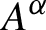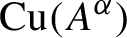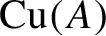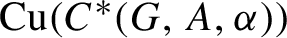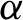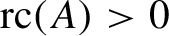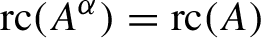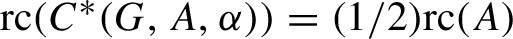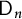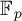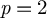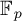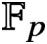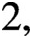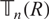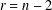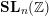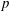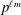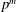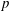Refine listing
Actions for selected content:
181 results in 19xxx
RECIPROCITY SHEAVES AND THEIR RAMIFICATION FILTRATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 19 March 2021, pp. 71-144
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
The Cuntz semigroup and the radius of comparison of the crossed product by a finite group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 10 March 2021, pp. 3541-3592
- Print publication:
- December 2021
-
- Article
- Export citation
Deformation of Dirac operators along orbits and quantization of noncompact Hamiltonian torus manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 1062-1092
- Print publication:
- August 2022
-
- Article
- Export citation
McKay matrices for finite-dimensional Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 686-731
- Print publication:
- June 2022
-
- Article
- Export citation
Twisted Donaldson invariants
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 04 February 2021, pp. 515-568
- Print publication:
- November 2021
-
- Article
- Export citation
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
The categorified Grothendieck–Riemann–Roch theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 154-214
- Print publication:
- January 2021
-
- Article
- Export citation
A weak Lefschetz result for Chow groups of complete intersections
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1014-1023
- Print publication:
- December 2021
-
- Article
- Export citation
ISOTROPIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1271-1330
- Print publication:
- July 2022
-
- Article
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation
A cancellation theorem for modules over integral group rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 27 November 2020, pp. 317-327
- Print publication:
- September 2021
-
- Article
- Export citation
Motivic Steenrod operations in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e52
-
- Article
-
- You have access
- Open access
- Export citation
DIRAC OPERATORS ON ORIENTIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 167-168
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
TOPOLOGIES ON SCHEMES AND MODULUS PAIRS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 13 July 2020, pp. 283-313
- Print publication:
- December 2021
-
- Article
- Export citation
A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 May 2020, pp. 1153-1170
- Print publication:
- August 2021
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
ANNIHILATOR-STABILITY AND TWO QUESTIONS OF NICHOLSON
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 April 2020, pp. 258-265
- Print publication:
- May 2021
-
- Article
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
Stability in the high-dimensional cohomology of congruence subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 822-861
- Print publication:
- April 2020
-
- Article
- Export citation
Essential Dimension, Symbol Length and
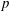 $p$-rank
$p$-rank
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 882-890
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation