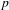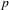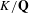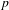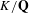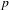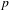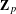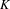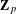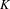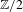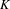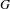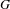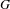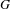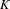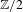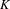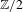Refine listing
Actions for selected content:
181 results in 19xxx
TOPOLOGICAL STATES OF MATTER AND NONCOMMUTATIVE GEOMETRY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 21 July 2016, p. 349
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Reciprocity sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1851-1898
- Print publication:
- September 2016
-
- Article
- Export citation
Motivic cohomology spectral sequence and Steenrod operations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 24 June 2016, pp. 2113-2133
- Print publication:
- October 2016
-
- Article
- Export citation
Mirković–Vilonen polytopes and Khovanov–Lauda–Rouquier algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 1648-1696
- Print publication:
- August 2016
-
- Article
- Export citation
NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 24 May 2016, pp. 785-821
- Print publication:
- September 2018
-
- Article
- Export citation
IMAGES OF QUANTUM REPRESENTATIONS OF MAPPING CLASS GROUPS AND DUPONT–GUICHARDET–WIGNER QUASI-HOMOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 27 January 2016, pp. 277-304
- Print publication:
- April 2018
-
- Article
- Export citation
LORENTZIAN GEOMETRY AND PHYSICS IN KASPAROV’S THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 21 January 2016, pp. 340-341
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Symmetric operations for all primes and Steenrod operations in algebraic cobordism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 1052-1070
- Print publication:
- May 2016
-
- Article
- Export citation
The Brauer group and indecomposable
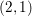 $(2,1)$-cycles
$(2,1)$-cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 1041-1051
- Print publication:
- May 2016
-
- Article
- Export citation
ON THE MOTIVIC SPECTRAL SEQUENCE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 25 November 2015, pp. 137-170
- Print publication:
- February 2018
-
- Article
- Export citation
Étale motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 556-666
- Print publication:
- March 2016
-
- Article
- Export citation
Topological K-theory of complex noncommutative spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 22 September 2015, pp. 489-555
- Print publication:
- March 2016
-
- Article
- Export citation
On exact
 $\infty$-categories and the Theorem of the Heart
$\infty$-categories and the Theorem of the Heart
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 2160-2186
- Print publication:
- November 2015
-
- Article
- Export citation
A Feynman integral via higher normal functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2329-2375
- Print publication:
- December 2015
-
- Article
- Export citation
Positive Curvature, Partial Vanishing Theorems and Coarse Indices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 223-233
-
- Article
- Export citation
ON THE WEAK GROTHENDIECK GROUP OF A BEZOUT RING
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 617-635
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
EQUIVARIANT ANDERSON DUALITY AND MACKEY FUNCTOR DUALITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 649-676
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
The Green Rings of Minimal Hopf Quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 June 2015, pp. 107-141
-
- Article
- Export citation
ON THE NON-TRIVIALITY OF THE
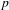 $p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO
$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 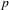 $p$ , II: SHIMURA CURVES
$p$ , II: SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 189-222
- Print publication:
- February 2017
-
- Article
- Export citation
EQUIVARIANT CALCULUS OF FUNCTORS AND
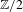 $\mathbb{Z}/2$ -ANALYTICITY OF REAL ALGEBRAIC
$\mathbb{Z}/2$ -ANALYTICITY OF REAL ALGEBRAIC 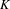 $K$ -THEORY
$K$ -THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 01 April 2015, pp. 829-883
- Print publication:
- October 2016
-
- Article
- Export citation
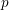
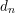
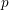
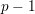
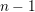
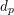
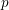
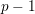
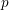
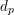
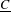

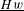
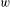
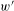
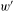
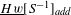
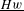

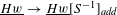

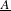
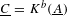
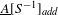
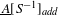
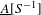

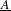
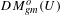
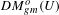
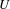
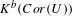
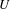
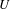

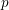
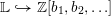
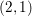
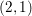
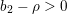
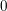
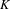
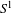
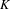
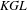
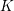
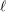
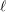
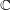
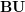
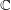
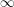
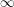
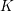
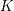
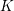
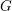
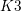
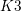
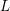
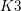
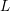
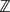
 be a field and let
be a field and let 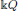 . Tensor categories of the form rep
. Tensor categories of the form rep