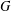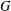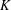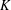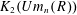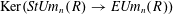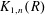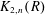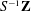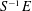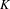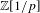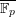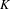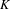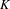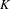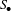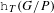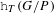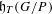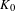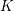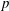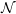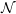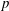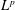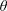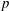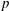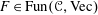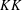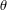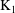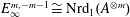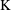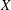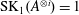Refine listing
Actions for selected content:
181 results in 19xxx
THE INTERSECTION MOTIVE OF THE MODULI STACK OF SHTUKAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 February 2020, e8
-
- Article
-
- You have access
- Open access
- Export citation
GLOBAL ACTIONS AND VECTOR
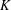 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 15 January 2020, e4
-
- Article
-
- You have access
- Open access
- Export citation
CATEGORIFYING RATIONALIZATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 January 2020, e42
-
- Article
-
- You have access
- Open access
- Export citation
RIGIDITY FOR RIGID ANALYTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1341-1369
- Print publication:
- July 2021
-
- Article
- Export citation
tt-geometry of Tate motives over algebraically closed fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1888-1923
- Print publication:
- October 2019
-
- Article
- Export citation
The Category of Ordered Bratteli Diagrams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1-28
- Print publication:
- February 2021
-
- Article
- Export citation
EQUIVARIANT ALGEBRAIC INDEX THEOREM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 929-955
- Print publication:
- May 2021
-
- Article
- Export citation
HIGHER
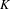 $K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
$K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1205-1273
- Print publication:
- July 2021
-
- Article
- Export citation
Open manifolds with non-homeomorphic positively curved souls
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 357-376
- Print publication:
- September 2020
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
TOWARDS A NON-ARCHIMEDEAN ANALYTIC ANALOG OF THE BASS–QUILLEN CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1931-1946
- Print publication:
- November 2020
-
- Article
- Export citation
CHERN CLASSES WITH MODULUS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 84-133
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
POSITIVE SCALAR CURVATURE AND CALLIAS-TYPE INDEX THEOREMS FOR PROPER ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 342-343
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Spectral Flow Argument Localizing an Odd Index Pairing
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 373-381
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Integral Formula for Spectral Flow for
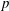 $p$-Summable Operators
$p$-Summable Operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 337-379
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Monoidal Categories, 2-Traces, and Cyclic Cohomology
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 293-312
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED
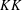 $KK$-THEORY
$KK$-THEORY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-180
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Factorizations in Bounded Hereditary Noetherian Prime Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 395-442
-
- Article
- Export citation
The Coniveau Filtration on
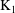 $\text{K}_{1}$ for Some Severi–Brauer Varieties
$\text{K}_{1}$ for Some Severi–Brauer Varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 24 October 2018, pp. 565-576
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A CONSTRUCTION OF SURFACES WITH LARGE HIGHER CHOW GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 311-331
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation