Refine listing
Actions for selected content:
181 results in 19xxx
Box splines and the equivariant index theorem
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 01 June 2012, pp. 503-544
- Print publication:
- July 2013
-
- Article
- Export citation
The slice Burnside ring and the section Burnside ring of a finite group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 22 March 2012, pp. 868-906
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
From L-series of elliptic curves to Mahler measures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 23 January 2012, pp. 385-414
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Mixed motives over k[t]/(tm+1)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 611-657
- Print publication:
- July 2012
-
- Article
- Export citation
ℤ[1/p]-motivic resolution of singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 1434-1446
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Non-connective K-theory via universal invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1281-1320
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
FAMILIES OF DIRAC OPERATORS AND QUANTUM AFFINE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 213-220
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
A p-adic analogue of the Borel regulator and the Bloch–Kato exponential map
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 149-190
- Print publication:
- January 2011
-
- Article
- Export citation
L'invariant de Suslin en caractéristique positive
- Part of
-
- Journal:
- Journal of K-Theory / Volume 5 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 559-602
- Print publication:
- June 2010
-
- Article
- Export citation
Hochschild cohomology of tensor products of topological algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 447-470
-
- Article
-
- You have access
- Export citation
On descent theory and main conjectures in non-commutative Iwasawa theory
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 26 April 2010, pp. 59-118
- Print publication:
- January 2011
-
- Article
- Export citation
Motives of Azumaya algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 14 April 2010, pp. 481-599
- Print publication:
- July 2010
-
- Article
- Export citation
Chow motives without projectivity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 04 September 2009, pp. 1196-1226
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Morita equivalences and KK-theory for Banach algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 565-593
- Print publication:
- July 2009
-
- Article
- Export citation
Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky versus Hanamura
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 39-97
- Print publication:
- January 2009
-
- Article
- Export citation
Determining Fitting ideals of minus class groups via the equivariant Tamagawa number conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1399-1426
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Cohomological characterization of the Hilbert symbol over Q*p
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-368
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Equivariant KK-theory for inverse limits of G-C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-211
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
The Toeplitz operator proof of noncommutative Bott periodicity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-251
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Symplectic complex bundles over real algebraic four-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 430-437
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
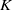
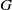
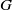
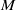
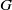
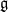
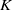
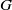
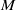
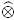 -algebras which are Fréchet spaces or nuclear
-algebras which are Fréchet spaces or nuclear  (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM
(and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM (
(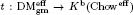 ;
; 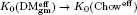 . A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if
. A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if 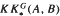 are extended to the setting of inverse limits of
are extended to the setting of inverse limits of 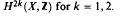 .
.