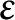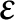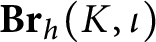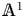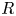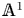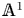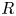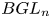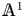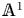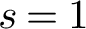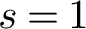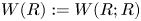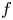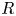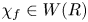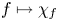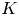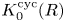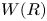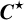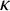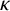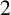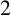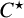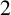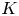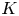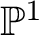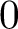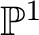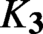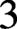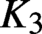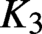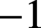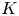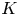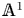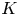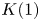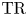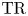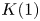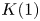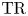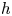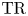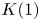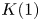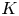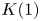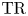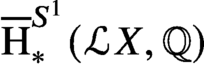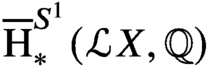Refine listing
Actions for selected content:
181 results in 19xxx
Mixed Witt rings of algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 March 2022, pp. 608-644
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Localization and nilpotent spaces in
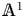 ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 654-720
- Print publication:
- March 2022
-
- Article
- Export citation
Trace and Künneth formulas for singularity categories and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 483-528
- Print publication:
- March 2022
-
- Article
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
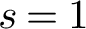 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 2241-2295
- Print publication:
- September 2023
-
- Article
- Export citation
Witt vectors with coefficients and characteristic polynomials over non-commutative rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 366-408
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological models for stable motivic invariants of regular number rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 January 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE K-THEORY OF THE
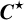 ${\mathit{C}}^{\star }$-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
${\mathit{C}}^{\star }$-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 119-144
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-crossings and a categorification of K-theory stable bases of the Springer resolution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2341-2376
- Print publication:
- November 2021
-
- Article
- Export citation
De Rham–Witt sheaves via algebraic cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 2089-2132
- Print publication:
- October 2021
-
- Article
- Export citation
THE ZEROTH
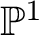 $\mathbb P^1$-STABLE HOMOTOPY SHEAF OF A MOTIVIC SPACE
$\mathbb P^1$-STABLE HOMOTOPY SHEAF OF A MOTIVIC SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1293-1317
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOREL CHARACTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 July 2021, pp. 747-797
- Print publication:
- March 2023
-
- Article
- Export citation
EULER CLASSES: SIX-FUNCTORS FORMALISM, DUALITIES, INTEGRALITY AND LINEAR SUBSPACES OF COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 16 July 2021, pp. 681-746
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counterexamples to Hochschild-Kostant-Rosenberg in characteristic p
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 June 2021, e49
-
- Article
-
- You have access
- Open access
- Export citation
Homology and K-theory of dynamical systems I. Torsion-free ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 2630-2660
- Print publication:
- August 2022
-
- Article
- Export citation
Hyperbolic tessellations and generators of
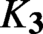 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
K-theory of valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1121-1142
- Print publication:
- June 2021
-
- Article
- Export citation
Towards Vorst's conjecture in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1143-1171
- Print publication:
- June 2021
-
- Article
- Export citation
On
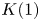 $K(1)$-local
$K(1)$-local 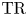 $\mathrm {TR}$
$\mathrm {TR}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1079-1119
- Print publication:
- May 2021
-
- Article
- Export citation
Hodge decomposition of string topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 April 2021, e33
-
- Article
-
- You have access
- Open access
- Export citation