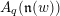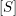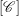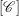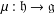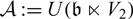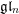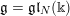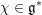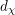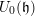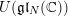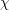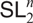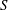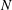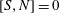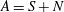Refine listing
Actions for selected content:
267 results in 17Bxx
Laurent phenomenon and simple modules of quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2263-2295
- Print publication:
- December 2019
-
- Article
- Export citation
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
- Export citation
Minimal-dimensional representations of reduced enveloping algebras for
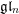 $\mathfrak{g}\mathfrak{l}_{n}$
$\mathfrak{g}\mathfrak{l}_{n}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1594-1617
- Print publication:
- August 2019
-
- Article
- Export citation
α-TYPE CHEVALLEY–EILENBERG COHOMOLOGY OF HOM-LIE ALGEBRAS AND BIALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. S108-S127
- Print publication:
- December 2020
-
- Article
- Export citation
JORDAN BIMODULES OVER THE SUPERALGEBRA M1|1
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 14 June 2019, pp. S6-S13
- Print publication:
- December 2020
-
- Article
- Export citation
CLUSTER CATEGORIES FROM GRASSMANNIANS AND ROOT COMBINATORICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 322-354
- Print publication:
- December 2020
-
- Article
- Export citation
ON REPRESENTATIONS OF SYMMETRIC LEIBNIZ ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 23 May 2019, pp. S99-S107
- Print publication:
- December 2020
-
- Article
- Export citation
Einstein–Maxwell Equations on Four-dimensional Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 09 May 2019, pp. 822-840
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
CODES, S-STRUCTURES, AND EXCEPTIONAL LIE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. S14-S27
- Print publication:
- December 2020
-
- Article
- Export citation
PARABOLIC SUBROOT SYSTEMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 355-366
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
A Basis Theorem for the Degenerate Affine Oriented Brauer–Clifford Supercategory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1061-1101
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Jordan–Chevalley Decomposition in Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 28 February 2019, pp. 349-354
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
The Cohomology Groups of Real Toric Varieties Associated with Weyl Chambers of Types C and D
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 861-874
-
- Article
- Export citation
On two cohomological Hall algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1581-1607
- Print publication:
- June 2020
-
- Article
- Export citation
On the Weak Order of Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 299-336
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Deformations of Pairs (Manifold, Coherent Sheaf)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1209-1241
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Two-color Soergel Calculus and Simple Transitive 2-representations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1523-1566
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
PBW Bases and Marginally Large Tableaux in Types B and C
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 37-54
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A CLASS OF QUASITRIANGULAR GROUP-COGRADED MULTIPLIER HOPF ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 December 2018, pp. 43-57
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation