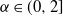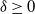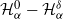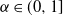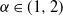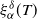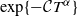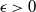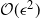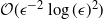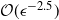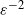Refine listing
Actions for selected content:
236 results in 65Cxx
Non-asymptotic analysis of Langevin-type Monte Carlo algorithms
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
(Empirical) Gramian-based dimension reduction for stochastic differential equations driven by fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the variance reduction of Hamiltonian Monte Carlo via an approximation scheme
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-27
-
- Article
- Export citation
How to beat a Bayesian adversary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 37 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 28 March 2025, pp. 73-95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perturbation theory for killed Markov processes and quasi-stationary distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1138-1165
- Print publication:
- September 2025
-
- Article
- Export citation
MICRO-MACRO PARAREAL, FROM ORDINARY DIFFERENTIAL EQUATIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS AND BACK AGAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e13
-
- Article
- Export citation
Optimal convergence rates of MCMC integration for functions with unbounded second moment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1069-1075
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence speed and approximation accuracy of numerical MCMC
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 101-133
- Print publication:
- March 2025
-
- Article
- Export citation
Early warning signs for SPDEs with continuous spectrum
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 665-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite element approximations for stochastic control problems with unbounded state space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 367-394
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stochastic gradient descent for barycenters in Wasserstein space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 September 2024, pp. 15-43
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the speed of convergence of discrete Pickands constants to continuous ones
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 111-135
- Print publication:
- March 2025
-
- Article
- Export citation
Error bounds for one-dimensional constrained Langevin approximations for nearly density-dependent Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 July 2024, pp. 825-867
- Print publication:
- September 2024
-
- Article
- Export citation
Convergence of hybrid slice sampling via spectral gap
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 July 2024, pp. 1440-1466
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1196-1198
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Antithetic multilevel particle filters
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1400-1439
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PDMP Monte Carlo methods for piecewise smooth densities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1153-1194
- Print publication:
- December 2024
-
- Article
- Export citation
Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 12 January 2024, pp. 503-538
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MONTE CARLO VARIANCE REDUCTION METHODS WITH APPLICATIONS IN STRUCTURAL RELIABILITY ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 518-521
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
A Monte Carlo algorithm for the extrema of tempered stable processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 1362-1389
- Print publication:
- December 2023
-
- Article
- Export citation