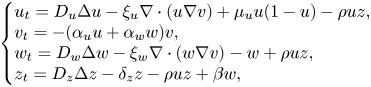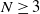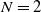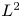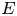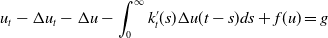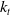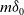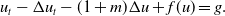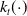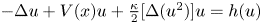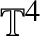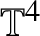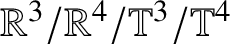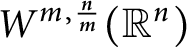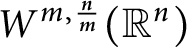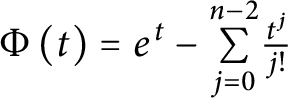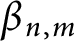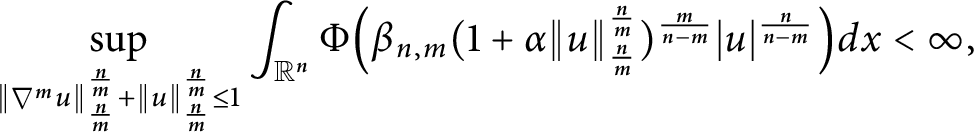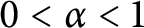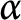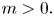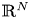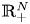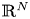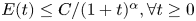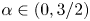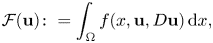Refine listing
Actions for selected content:
562 results in 35-XX
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 881-906
- Print publication:
- June 2023
-
- Article
- Export citation
A pinching estimate for convex hypersurfaces evolving under a non-homogeneous variant of mean curvature flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 376-391
-
- Article
- Export citation
Existence of solution for a class of activator–inhibitor systems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 April 2022, pp. 98-113
- Print publication:
- January 2023
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Corrigendum: Dynamics of a susceptible—infected—susceptible epidemic reaction—diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 718-720
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 764-783
- Print publication:
- June 2023
-
- Article
- Export citation
ELECTRICAL IMPEDANCE TOMOGRAPHY USING NONCONFORMING MESH AND POSTERIOR APPROXIMATED REGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 520-522
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
The nonclassical diffusion equations with time-dependent memory kernels and a new class of nonlinearities
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 February 2022, pp. 716-733
- Print publication:
- September 2022
-
- Article
- Export citation
Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 279-301
-
- Article
- Export citation
A SIMPLE AND NEARLY OPTIMAL INVESTMENT STRATEGY TO MINIMIZE THE PROBABILITY OF LIFETIME RUIN
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 52 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 February 2022, pp. 619-643
- Print publication:
- May 2022
-
- Article
- Export citation
Bifurcation of elastic curves with modulated stiffness
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 28-54
-
- Article
-
- You have access
- HTML
- Export citation
Necessary and sufficient conditions on global solvability for the p-k-Hessian inequalities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1004-1019
- Print publication:
- December 2022
-
- Article
- Export citation
Unconditional uniqueness for the energy-critical nonlinear Schrödinger equation on
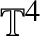 $\mathbb {T}^{4}$
$\mathbb {T}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation
Optimal Hardy-weights for the (p, A)-Laplacian with a potential term
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 December 2021, pp. 289-306
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
A sharpened form of Adams-type inequalities on higher-order Sobolev spaces
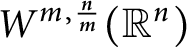 $W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
$W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 895-905
- Print publication:
- December 2022
-
- Article
- Export citation
Liouville-type results for positive solutions of pseudo-relativistic Schrödinger system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 196-228
- Print publication:
- February 2023
-
- Article
- Export citation
Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 167-176
- Print publication:
- February 2023
-
- Article
- Export citation
Partial regularity for minimizers of discontinuous quasiconvex integrals with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1191-1232
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation