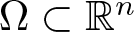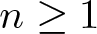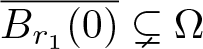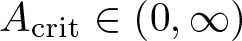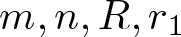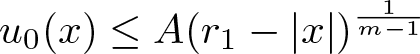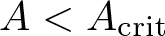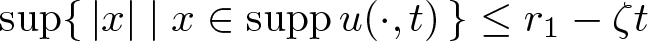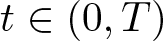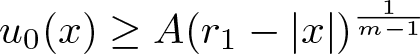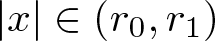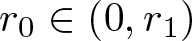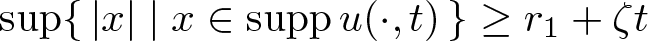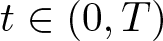Refine listing
Actions for selected content:
570 results in 35-XX
Normalized solutions for p-Laplacian equation with general nonlinearities on bounded domain
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-31
-
- Article
- Export citation
Nonlocal carrier’s double phase problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-24
-
- Article
- Export citation
General rogue waves of infinite order: exact properties, asymptotic behaviour, and effective numerical computation
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 13 November 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a Cahn–Hilliard equation for the growth and division of chemically active droplets modelling protocells
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-degeneracy and local uniqueness of bubbling solutions for fractional almost critical problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-45
-
- Article
- Export citation
Concentration behavior of normalized ground states for mass critical Kirchhoff equations in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-44
-
- Article
- Export citation
DYNAMICS OF NONLOCAL KURAMOTO–SIVASHINSHY EQUATIONS WITH MULTIPLICATIVE WHITE NOISE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 23 October 2025, e34
-
- Article
-
- You have access
- HTML
- Export citation
Normalized multi-bump solutions of nonlinear Hartree equation with steep potential well
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-37
-
- Article
- Export citation
A k-Hessian equation with a power nonlinearity source and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-25
-
- Article
- Export citation
Impact of birth pulse and environment shift on population survival and propagation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-27
-
- Article
- Export citation
A remark on the long-time asymptotics of global-in-time solutions for semilinear parabolic equations in
 ${\mathbb {R}^N}$
${\mathbb {R}^N}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-21
-
- Article
- Export citation
Global smooth solutions and singularity formation for the relativistic Euler equations with radial symmetry
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-32
-
- Article
- Export citation
Shrinking vs. expanding: the evolution of spatial support in degenerate Keller–Segel systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tunable localisation in parity-time-symmetric resonator arrays with imaginary gauge potentials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 September 2025, e157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A geometric approach to pinned pulses in a class of non-autonomous reaction–diffusion equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth solutions to the Christoffel–Minkowski problem in hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-29
-
- Article
- Export citation
Optimal boundary regularity of proper harmonic maps between asymptotically hyperbolic spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-38
-
- Article
- Export citation
Blow-up of cylindrically symmetric solutions for fractional NLS
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ill-posedness issue on the Oldroyd-B model in the critical Besov spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-20
-
- Article
- Export citation
Existence and nonexistence of least energy positive solutions to critical Schrödinger systems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-50
-
- Article
- Export citation