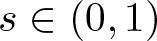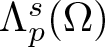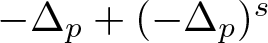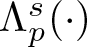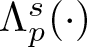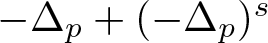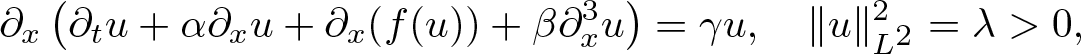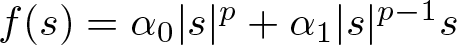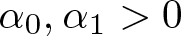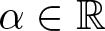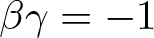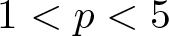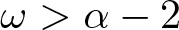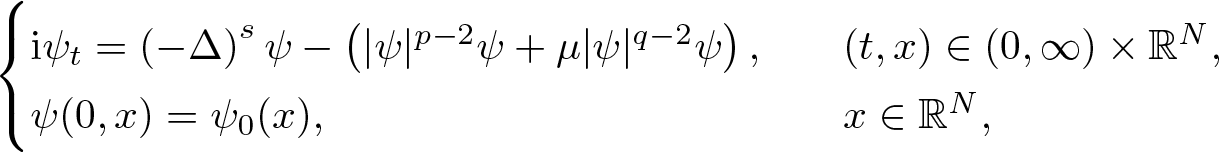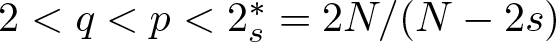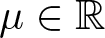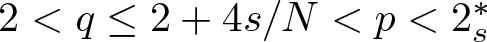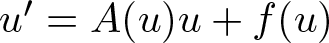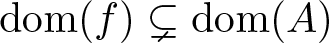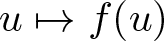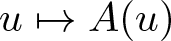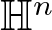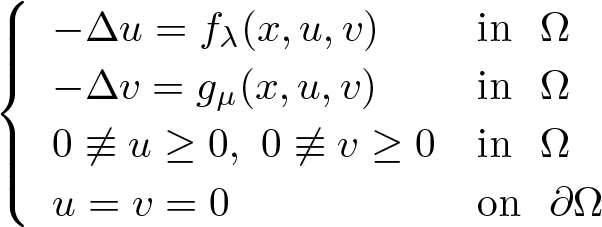Refine listing
Actions for selected content:
570 results in 35-XX
Well-posedness for the 3-D generalized micropolar system in critical Fourier–Besov–Morrey spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 891-907
- Print publication:
- September 2025
-
- Article
- Export citation
An elliptic operator with a nonlocal term: maximum principle, principal eigenvalue, and applications to a logistic equation with indefinite weight
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-38
-
- Article
- Export citation
Global well-posedness and Turing–Hopf bifurcation of prey-taxis systems with hunting cooperation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1121-1147
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple solutions for some classes of non-linear elliptic equations with variable exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-51
-
- Article
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
Models for information propagation on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1040-1061
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strict Faber–Krahn-type inequality for the mixed local–nonlocal operator under polarization
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 506-525
-
- Article
- Export citation
Harnack type estimates to non-linear elliptic systems in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-14
-
- Article
- Export citation
Spatio-temporal behaviour of SIR models with cross-diffusion and vital dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 972-992
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 172-183
- Print publication:
- August 2025
-
- Article
- Export citation
Analysis of a model describing bacterial colony expansion in radial geometry driven by chemotaxis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 910-947
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the Winterbottom shape
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral stability of constrained solitary waves for a generalized Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-32
-
- Article
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
- Export citation
Local regularity for nonlocal double phase equations in the Heisenberg group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-37
-
- Article
- Export citation
Asymptotic estimate of solutions in a 4th-order parabolic equation with the Frobenius norm of a Hessian matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 91-108
- Print publication:
- March 2025
-
- Article
- Export citation
Existence and non-existence results for a class of systems under concave-convex nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 128-156
-
- Article
- Export citation
Global well-posedness and uniform boundedness of 2D urban crime models with nonlinear advection enhancement
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 897-909
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and analyticity of solutions of the Kuramoto–Sivashinsky equation with singular data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-26
-
- Article
- Export citation