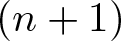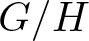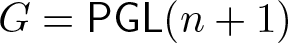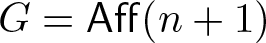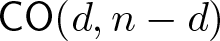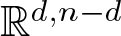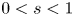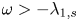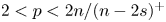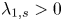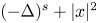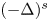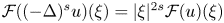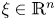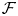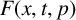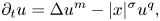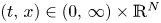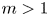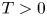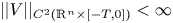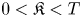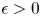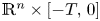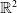Refine listing
Actions for selected content:
570 results in 35-XX
Projectively and affinely invariant PDEs on hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 714-739
-
- Article
- Export citation
Modelling of the fluid flow in a thin domain with injection through permeable boundary
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 776-796
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and symmetry breaking results for positive solutions of elliptic Hamiltonian systems
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1459-1487
- Print publication:
- October 2025
-
- Article
- Export citation
Propagation of anisotropic Gabor wave front sets
- Part of
- Partial differential equations
- Integral, integro-differential, and pseudodifferential operators
- General quantum mechanics and problems of quantization
- Groups and semigroups of linear operators, their generalizations and applications
- Partial differential equations on manifolds; differential operators
- Miscellaneous topics - Partial differential equations
- Distributions, generalized functions, distribution spaces
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 674-698
-
- Article
- Export citation
Slow passage through the Busse balloon – predicting steps on the Eckhaus staircase
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness and Hyers–Ulam’s stability for a fractional nonlinear partial integro-differential equation with variable coefficients and a mixed boundary condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1377-1397
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the fractional powers of a Schrödinger operator with a Hardy-type potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 460-507
-
- Article
- Export citation
Uniqueness of ground states to fractional nonlinear elliptic equations with harmonic potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-14
-
- Article
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-24
-
- Article
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 345-374
- Print publication:
- December 2024
-
- Article
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-22
-
- Article
- Export citation
Decay at infinity for solutions to some fractional parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-37
-
- Article
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1938-1959
- Print publication:
- October 2025
-
- Article
- Export citation
Unbounded Sturm attractors for quasilinear parabolic equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 542-565
-
- Article
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1661-1676
- Print publication:
- October 2025
-
- Article
- Export citation
Global dynamics and spatiotemporal heterogeneity of a preytaxis model with prey-induced acceleration
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 601-633
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1385-1430
- Print publication:
- August 2025
-
- Article
- Export citation
The fully parabolic multi-species chemotaxis system in
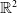 $\mathbb{R}^{2}$
$\mathbb{R}^{2}$
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 675-706
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multidimensional Frank–Laptev–Weidl improvement of the hardy inequality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 151-167
-
- Article
- Export citation
Persistence and the Sheaf-Function Correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation