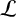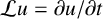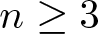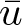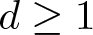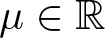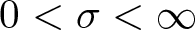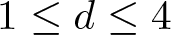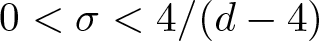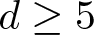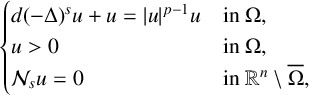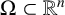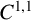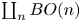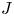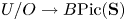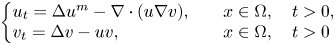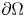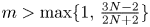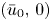Refine listing
Actions for selected content:
570 results in 35-XX
GRADIENT ESTIMATES FOR POSITIVE EIGENFUNCTIONS OF THE
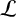 $\mathcal {L}$-OPERATOR ON CONFORMAL SOLITONS AND THEIR APPLICATIONS
$\mathcal {L}$-OPERATOR ON CONFORMAL SOLITONS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 344-355
- Print publication:
- April 2025
-
- Article
- Export citation
Liouville theorems for the sub-linear Lane–Emden equation on the half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-13
-
- Article
- Export citation
Dynamical behaviour of a logarithmically sensitive chemotaxis model under time-dependent boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 November 2024, pp. 638-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A diffusive plant-sulphide model: spatio-temporal dynamics contrast between discrete and distributed delay
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 811-828
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 1. The Cauchy problem on the real line
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 25 October 2024, pp. 775-810
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a weighted anisotropic eigenvalue problem
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 October 2024, pp. 72-85
- Print publication:
- January 2025
-
- Article
- Export citation
Travelling wavefronts for the Belousov–Zhabotinsky system with non-local delayed interaction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 738-774
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Blowup of cylindrically symmetric solutions for biharmonic NLS
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1085-1098
-
- Article
- Export citation
EMBED IN ENSEMBLE TO RIGOROUSLY AND ACCURATELY HOMOGENIZE QUASI-PERIODIC MULTI-SCALE HETEROGENEOUS MATERIAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a supersonic-sonic patch arising from the two-dimensional Riemann problem of the compressible Euler equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-40
-
- Article
- Export citation
Stabilization in a chemotaxis system modelling T-cell dynamics with simultaneous production and consumption of signals
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 570-583
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 178-209
- Print publication:
- April 2025
-
- Article
- Export citation
Numerical analysis of physics-informed neural networks and related models in physics-informed machine learning
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 633-713
-
- Article
-
- You have access
- Open access
- Export citation
A Hamiltonian ∐n BO(n)-action, stratified Morse theory and the J-homomorphism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2005-2099
- Print publication:
- September 2024
-
- Article
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
- Export citation
Opinion formation on evolving network: the DPA method applied to a nonlocal cross-diffusion PDE-ODE system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 748-775
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A global higher regularity result for the static relaxed micromorphic model on smooth domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Diffuse-interface approximation and weak–strong uniqueness of anisotropic mean curvature flow
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 82-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 May 2024, pp. 40-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
- Export citation