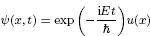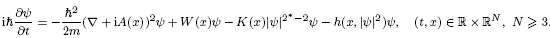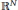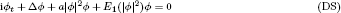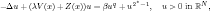Refine listing
Actions for selected content:
561 results in 35-XX
HÖLDER ESTIMATES FOR LINEAR SECOND-ORDER EQUATIONS: CORRIGENDUM
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 18 May 2011, p. 328
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
The Stokes Structure of a good meromorphic flat bundle
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 03 May 2011, pp. 675-712
- Print publication:
- July 2011
-
- Article
- Export citation
Very slow grow-up of solutions of a semi-linear parabolic equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 381-400
-
- Article
-
- You have access
- Export citation
HÖLDER ESTIMATES FOR LINEAR SECOND-ORDER EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 315-327
- Print publication:
- July 2011
-
- Article
- Export citation
Solutions of perturbed Schrödinger equations with electromagnetic fields and critical nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 131-147
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
THE LARGE-TIME SOLUTION OF A NONLINEAR FOURTH-ORDER EQUATION INITIAL-VALUE PROBLEM I. INITIAL DATA WITH A DISCONTINUOUS EXPANSIVE STEP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 18 May 2010, pp. 178-190
-
- Article
-
- You have access
- Export citation
Interior h1 Estimates for Parabolic Equations with LMO Coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-217
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Solutions for Semilinear Elliptic Systems with Critical Sobolev Exponent and Hardy Potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-33
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
ON A PERTURBED CONSERVATIVE SYSTEM OF SEMILINEAR WAVE EQUATIONS WITH PERIODIC-DIRICHLET BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 281-288
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Spectral Convergence for High-Contrast Elliptic Periodic Problems with a Defect Via Homogenization
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 29-57
- Print publication:
- December 2009
-
- Article
- Export citation
Unstable sets, heteroclinic orbits and generic quasi-convergence for essentially strongly order-preserving semiflows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 797-807
-
- Article
-
- You have access
- Export citation
Critical extinction and blow-up exponents for fast diffusive polytropic filtration equation with sources
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 419-444
-
- Article
-
- You have access
- Export citation
Generalized oscillatory integrals and Fourier integral operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 351-386
-
- Article
-
- You have access
- Export citation
A cross-constrained variational problem for the generalized Davey–Stewartson system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 67-77
-
- Article
-
- You have access
- Export citation
Multiplicity of positive solutions for a class of problems with critical growth in ℝN
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 1-21
-
- Article
-
- You have access
- Export citation
On application of kinetic formulation of the Le Roux system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 263-272
-
- Article
-
- You have access
- Export citation
ON SCHRÖDINGER EQUATIONS WITH INDEFINITE NONLINEARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 115-128
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Regularity at space-like and null infinity
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-208
- Print publication:
- January 2009
-
- Article
- Export citation
NEW GRONWALL–OU-IANG TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 111-127
-
- Article
-
- You have access
- Export citation