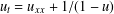Refine listing
Actions for selected content:
562 results in 35-XX
Aspects of Hadamard well-posedness for classes of non-Lipschitz semilinear parabolic partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 777-832
- Print publication:
- August 2016
-
- Article
- Export citation
Dynamics of a susceptible–infected–susceptible epidemic reaction–diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 929-946
- Print publication:
- October 2016
-
- Article
- Export citation
Nodal vector solutions with clustered peaks for nonlinear elliptic equations in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 947-982
- Print publication:
- October 2016
-
- Article
- Export citation
Separation of variables in equations of mean-curvature type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1017-1035
- Print publication:
- October 2016
-
- Article
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
Semidefinite Optimization Estimating Bounds on Linear Functionals Defined on Solutions of Linear ODEs
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 599-615
- Print publication:
- August 2016
-
- Article
- Export citation
On a Class of Semilinear Elliptic Eigenvalue Problems in ℝ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 107-126
-
- Article
- Export citation
Periodic Navier Solutions for the Plate Equation with Non-Monotone Nonlinearities: the Multidimensional Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 203-230
-
- Article
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
- Print publication:
- June 2018
-
- Article
- Export citation
Concentration of solutions of equations of nonlinear Schrödinger type with vector potential: infinite-bump solutions and non-degeneracy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 625-646
- Print publication:
- June 2016
-
- Article
- Export citation
A convergence result for the ergodic problem for Hamilton–Jacobi equations with Neumann-type boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 225-242
- Print publication:
- April 2016
-
- Article
- Export citation
The existence of a ground-state solution for a class of Kirchhoff-type equations in ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 371-391
- Print publication:
- April 2016
-
- Article
- Export citation
Existence and multiplicity of solutions for an indefinite Kirchhoff-type equation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 435-448
- Print publication:
- April 2016
-
- Article
- Export citation
THE QUENCHING OF SOLUTIONS OF A REACTION–DIFFUSION EQUATION WITH FREE BOUNDARIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 110-120
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
MATHEMATICAL MODELS OF CALCIUM AND TIGHT JUNCTIONS IN NORMAL AND RECONSTRUCTED EPIDERMIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 347-349
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Solutions for a Kirchhoff Equation with Weight and Nonlinearity with Subcritical and Critical Caffarelli–Kohn–Nirenberg Growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 925-944
-
- Article
- Export citation
The regularity and stability of solutions to semilinear fourth-order elliptic problems with negative exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 195-212
- Print publication:
- February 2016
-
- Article
- Export citation
Short-time asymptotic expansions of semilinear evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 141-167
- Print publication:
- February 2016
-
- Article
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
- Print publication:
- 2016
-
- Article
- Export citation
Solutions of p-Laplace Equations with Infinite Boundary Values: The case of Non-Autonomous and Non-Monotone Nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 959-987
-
- Article
- Export citation
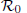 is defined for the model. We first prove that there exists a unique endemic equilibrium if
is defined for the model. We first prove that there exists a unique endemic equilibrium if 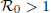 . We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if
. We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if 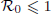 , while the endemic equilibrium is globally attractive if
, while the endemic equilibrium is globally attractive if 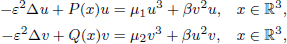
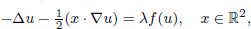
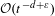
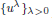 to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini
to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini 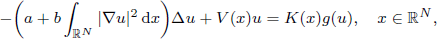
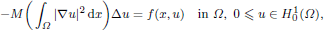
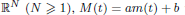 and
and 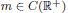 . We require that
. We require that