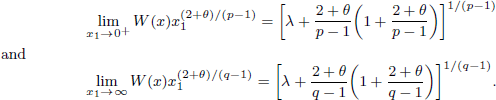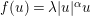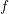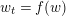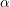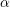Refine listing
Actions for selected content:
562 results in 35-XX
A rigidity result for non-local semilinear equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1009-1018
- Print publication:
- October 2017
-
- Article
- Export citation
Computing Residual Diffusivity by Adaptive Basis Learning via Spectral Method
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 351-372
- Print publication:
- May 2017
-
- Article
- Export citation
Linear Stability of Hyperbolic Moment Models for Boltzmann Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 255-277
- Print publication:
- May 2017
-
- Article
- Export citation
An evolutional free-boundary problem of a reaction–diffusion–advection system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 February 2017, pp. 615-648
- Print publication:
- June 2017
-
- Article
- Export citation
PERTURBATIONS FROM INDEFINITE SYMMETRIC ELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 February 2017, pp. 635-648
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Finite Element Solution for MHD Flow of Nanofluids with Heat and Mass Transfer through a Porous Media with Thermal Radiation, Viscous Dissipation and Chemical Reaction Effects
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 904-923
- Print publication:
- August 2017
-
- Article
- Export citation
Stability and Unstability of the Standing Wave to Euler Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 818-838
- Print publication:
- August 2017
-
- Article
- Export citation
Infinitely many non-radial solutions for the polyharmonic Hénon equation with a critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 371-396
- Print publication:
- April 2017
-
- Article
- Export citation
On the Hardy–Sobolev equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 299-336
- Print publication:
- April 2017
-
- Article
- Export citation
Neumann to Steklov eigenvalues: asymptotic and monotonicity results
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 429-447
- Print publication:
- April 2017
-
- Article
- Export citation
A Hardy–Sobolev inequality for the twisted Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1-23
- Print publication:
- February 2017
-
- Article
- Export citation
Existence results for semilinear problems in the two-dimensional hyperbolic space involving critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 141-176
- Print publication:
- February 2017
-
- Article
- Export citation
Coexistence Solutions for a Periodic Competition Model with Singular–Degenerate Diffusion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 1065-1075
-
- Article
- Export citation
Homogenization and norm-resolvent convergence for elliptic operators in a strip perforated along a curve
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1115-1158
- Print publication:
- December 2016
-
- Article
- Export citation
Optimal Hardy inequalities in cones
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 89-124
- Print publication:
- February 2017
-
- Article
- Export citation
Multiplicity of Multi-Bump Type Nodal Solutions for A Class of Elliptic Problems with Exponential Critical Growth in ℝ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 273-297
-
- Article
- Export citation
Asymptotic behaviour and symmetry of positive solutions to nonlinear elliptic equations in a half-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1243-1263
- Print publication:
- December 2016
-
- Article
- Export citation
NON-REGULARITY IN HÖLDER AND SOBOLEV SPACES OF SOLUTIONS TO THE SEMILINEAR HEAT AND SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 44-70
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
Uniqueness of the null solution to a nonlinear partial differential equation satisfied by the explosion probability of a branching diffusion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 938-945
- Print publication:
- September 2016
-
- Article
- Export citation
Asymptotic behaviour of the lifespan of solutions for a semilinear heat equation in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 1091-1114
- Print publication:
- October 2016
-
- Article
- Export citation
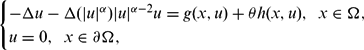
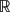

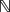
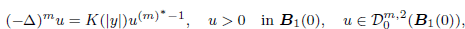
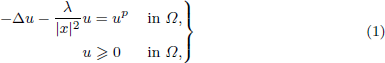
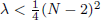 . Using a suitable map we transform problem (1) into another one without the singularity 1/|
. Using a suitable map we transform problem (1) into another one without the singularity 1/|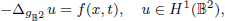
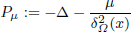
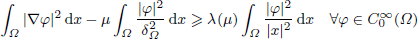
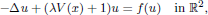
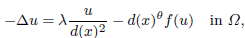
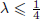 ,
,