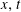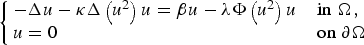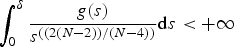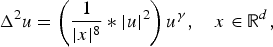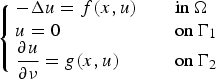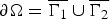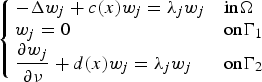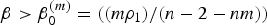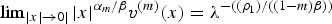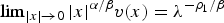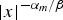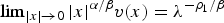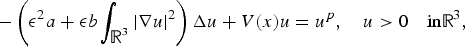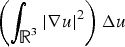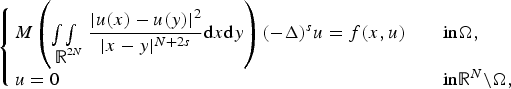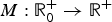Refine listing
Actions for selected content:
562 results in 35-XX
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 937-982
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Generalizing Hopf’s Boundary Point Lemma
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 183-197
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Bifurcation and standing wave solutions for a quasilinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 939-968
- Print publication:
- August 2019
-
- Article
- Export citation
Some nonexistence theorems for semilinear fourth-order equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 761-779
- Print publication:
- June 2019
-
- Article
- Export citation
Classification of nonnegative solutions to a bi-harmonic equation with Hartree type nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 979-994
- Print publication:
- August 2019
-
- Article
- Export citation
Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 305-324
- Print publication:
- April 2019
-
- Article
- Export citation
Singular limits and properties of solutions of some degenerate elliptic and parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 353-385
- Print publication:
- April 2019
-
- Article
- Export citation
A quantitative Carleman estimate for second-order elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 915-938
- Print publication:
- August 2019
-
- Article
- Export citation
Minimizing movements for oscillating energies: the critical regime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 719-737
- Print publication:
- June 2019
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
Multi-peak positive solutions to a class of Kirchhoff equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1097-1122
- Print publication:
- August 2019
-
- Article
- Export citation
Existence results for Kirchhoff–type superlinear problems involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1061-1081
- Print publication:
- August 2019
-
- Article
- Export citation
A mean field equation involving positively supported probability measures: blow-up phenomena and variational aspects
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 325-352
- Print publication:
- April 2019
-
- Article
- Export citation
Finite speed of disturbance for the nonlinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1405-1419
- Print publication:
- December 2019
-
- Article
- Export citation
Continuous solutions and approximating scheme for fractional Dirichlet problems on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 533-560
- Print publication:
- April 2019
-
- Article
- Export citation
HARDY AND RELLICH INEQUALITIES ON THE COMPLEMENT OF CONVEX SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 98-119
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Multiscale modelling and homogenisation of fibre-reinforced hydrogels for tissue engineering
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 22 November 2018, pp. 143-171
-
- Article
-
- You have access
- Export citation
THE UNIQUE CONTINUATION PROPERTY OF
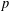 $p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
$p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 219-230
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Simulation of multiphase porous media flows with minimising movement and finite volume schemes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 1123-1152
-
- Article
- Export citation