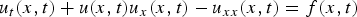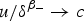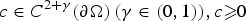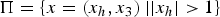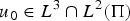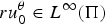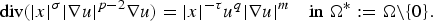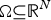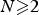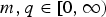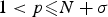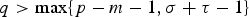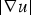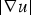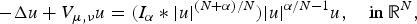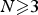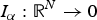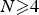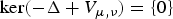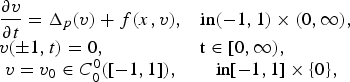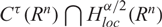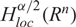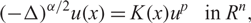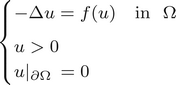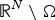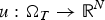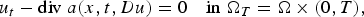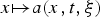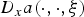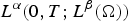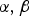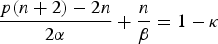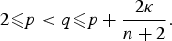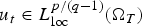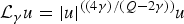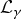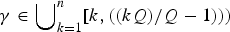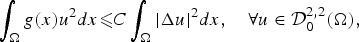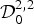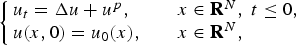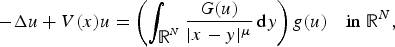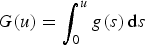Refine listing
Actions for selected content:
562 results in 35-XX
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 2025-2054
- Print publication:
- August 2020
-
- Article
- Export citation
A Hopf-type Boundary Point Lemma for Pairs of Solutions to Quasilinear Equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 22 February 2019, pp. 607-621
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Positive solutions of semilinear elliptic problems with a Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1791-1804
- Print publication:
- August 2020
-
- Article
- Export citation
Axisymmetric flows in the exterior of a cylinder
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1671-1698
- Print publication:
- August 2020
-
- Article
- Export citation
Decay rates at infinity for solutions to periodic Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1113-1126
- Print publication:
- June 2020
-
- Article
- Export citation
Gradient estimates for nonlinear elliptic equations with a gradient-dependent nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1361-1376
- Print publication:
- June 2020
-
- Article
- Export citation
Liouville-type theorems and existence results for stable solutions to weighted Lane–Emden equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1567-1579
- Print publication:
- June 2020
-
- Article
- Export citation
Groundstates for Choquard type equations with Hardy–Littlewood–Sobolev lower critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1377-1400
- Print publication:
- June 2020
-
- Article
- Export citation
Linearized stability implies dynamic stability for equilibria of 1-dimensional, p-Laplacian boundary value problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1313-1338
- Print publication:
- June 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
ON NONLOCAL NONLINEAR ELLIPTIC PROBLEMS WITH THE FRACTIONAL LAPLACIAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 75-84
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
A stability index for travelling waves in activator-inhibitor systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 517-548
- Print publication:
- February 2020
-
- Article
- Export citation
A note on a positive solution of a null mass nonlinear field equation in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 841-870
- Print publication:
- April 2020
-
- Article
- Export citation
On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p, q)-growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 419-451
- Print publication:
- February 2020
-
- Article
- Export citation
An application of the theorem on Sums to viscosity solutions of degenerate fully nonlinear equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 975-992
- Print publication:
- April 2020
-
- Article
- Export citation
Nodal solutions for the fractional Yamabe problem on Heisenberg groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 771-788
- Print publication:
- April 2020
-
- Article
- Export citation
On the generalized Hardy-Rellich inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 897-919
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotically self-similar behaviour of global solutions for semilinear heat equations with algebraically decaying initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 789-811
- Print publication:
- April 2020
-
- Article
- Export citation
Strong maximum principles for fractional elliptic and parabolic problems with mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 475-495
- Print publication:
- February 2020
-
- Article
- Export citation
Existence of solutions for critical Choquard equations via the concentration-compactness method
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 921-954
- Print publication:
- April 2020
-
- Article
- Export citation