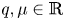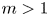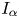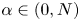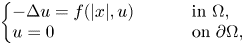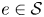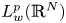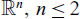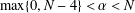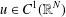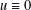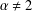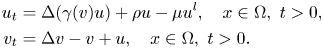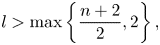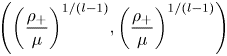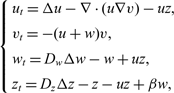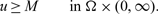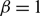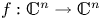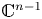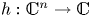Refine listing
Actions for selected content:
562 results in 35-XX
Localised signalling compartments in 2D coupled by a bulk diffusion field: Quorum sensing and synchronous oscillations in the well-mixed limit
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 10 August 2020, pp. 1001-1031
-
- Article
- Export citation
GLOBAL NEARLY-PLANE-SYMMETRIC SOLUTIONS TO THE MEMBRANE EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 05 August 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
Existence and two-scale convergence of the generalised Poisson–Nernst–Planck problem with non-linear interface conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 03 August 2020, pp. 683-710
-
- Article
-
- You have access
- Open access
- Export citation
Quasilinear elliptic inequalities with Hardy potential and nonlocal terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 July 2020, pp. 1075-1093
- Print publication:
- June 2021
-
- Article
- Export citation
A monotonicity result under symmetry and Morse index constraints in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 885-915
- Print publication:
- June 2021
-
- Article
- Export citation
On decay rates of the solutions of parabolic Cauchy problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 1021-1039
- Print publication:
- June 2021
-
- Article
- Export citation
Does indirectness of signal production reduce the explosion-supporting potential in chemotaxis–haptotaxis systems? Global classical solvability in a class of models for cancer invasion (and more)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 618-651
-
- Article
- Export citation
Fano resonance in metallic grating via strongly coupled subwavelength resonators
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 370-394
-
- Article
- Export citation
Global and exponential attractor of the repulsive Keller–Segel model with logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 599-617
-
- Article
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
- Export citation
An n-dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 29 May 2020, pp. 821-841
- Print publication:
- April 2021
-
- Article
- Export citation
A LIPSCHITZ METRIC FOR THE CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 May 2020, e27
-
- Article
-
- You have access
- Open access
- Export citation
Conditional symmetries and exact solutions of a nonlinear three-component reaction-diffusion model
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 May 2020, pp. 280-300
-
- Article
- Export citation
A critical virus production rate for efficiency of oncolytic virotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 May 2020, pp. 301-316
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Concentration of positive solutions for a class of fractional p-Kirchhoff type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 601-651
- Print publication:
- April 2021
-
- Article
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
Transition waves for lattice Fisher-KPP equations with time and space dependence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 April 2020, pp. 573-600
- Print publication:
- April 2021
-
- Article
- Export citation
Relaxation of the Cahn–Hilliard equation with singular single-well potential and degenerate mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 89-112
-
- Article
- Export citation
A novel Landau-de Gennes model with quartic elastic terms
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 177-198
-
- Article
- Export citation