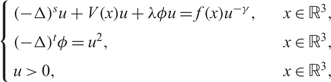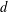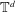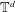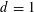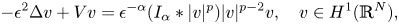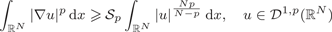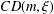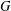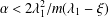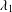Refine listing
Actions for selected content:
562 results in 35-XX
Hopf bifurcation from spike solutions for the weak coupling Gierer–Meinhardt system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 113-145
-
- Article
- Export citation
FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 179-192
- Print publication:
- January 2021
-
- Article
- Export citation
On approximating minimizers of convex functionals with a convexity constraint by singular Abreu equations without uniform convexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 356-376
- Print publication:
- February 2021
-
- Article
- Export citation
LONG TIME BEHAVIOR OF THE SOLUTIONS OF NLW ON THE
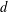 $d$-DIMENSIONAL TORUS
$d$-DIMENSIONAL TORUS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Multiple bound states of higher topological type for semi-classical Choquard equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 329-355
- Print publication:
- February 2021
-
- Article
- Export citation
Nondegeneracy of the bubble for the critical p-Laplace equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 151-168
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS ON FINITE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 477-487
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 2682-2718
- Print publication:
- October 2020
-
- Article
- Export citation
QUADRATIC DIFFERENTIAL EQUATIONS: PARTIAL GELFAND–SHILOV SMOOTHING EFFECT AND NULL-CONTROLLABILITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 31 January 2020, pp. 1749-1801
- Print publication:
- November 2021
-
- Article
- Export citation
Bilinear identities involving the k-plane transform and Fourier extension operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 January 2020, pp. 3349-3377
- Print publication:
- December 2020
-
- Article
- Export citation
Uniqueness and multiplicity of positive solutions for a diffusive predator–prey model in the heterogeneous environment
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 20 January 2020, pp. 3321-3348
- Print publication:
- December 2020
-
- Article
- Export citation
Existence, non-existence and blow-up behaviour of minimizers for the mass-critical fractional non-linear Schrödinger equations with periodic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3252-3292
- Print publication:
- December 2020
-
- Article
- Export citation
On Some Topological Properties of Fourier Transforms of Regular Holonomic
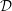 ${\mathcal{D}}$-Modules
${\mathcal{D}}$-Modules
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 06 January 2020, pp. 454-468
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
THE GLOBAL CAUCHY PROBLEM FOR THE NLS WITH HIGHER ORDER ANISOTROPIC DISPERSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 45-53
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation
Gradient estimates for the constant mean curvature equation in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 3216-3230
- Print publication:
- December 2020
-
- Article
- Export citation
On supercritical nonlinear Schrödinger equations with ellipse-shaped potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 02 December 2019, pp. 3187-3215
- Print publication:
- December 2020
-
- Article
- Export citation
Cops-on-the-dots: The linear stability of crime hotspots for a 1-D reaction-diffusion model of urban crime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 November 2019, pp. 871-917
-
- Article
- Export citation
Global minimisers for anisotropic attractive–repulsive interactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 22 October 2019, pp. 854-870
-
- Article
- Export citation
Homogenisation problems in reactive decontamination
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 782-805
-
- Article
- Export citation
Mass transport in Fokker–Planck equations with tilted periodic potential
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 709-736
-
- Article
- Export citation