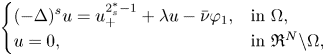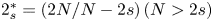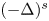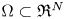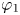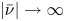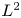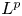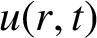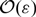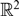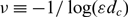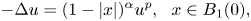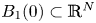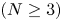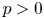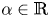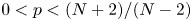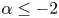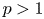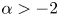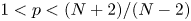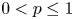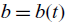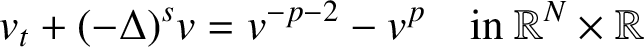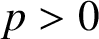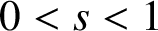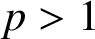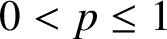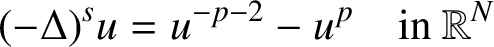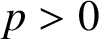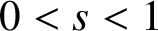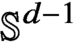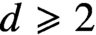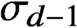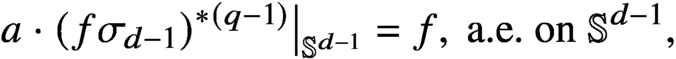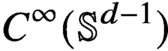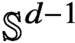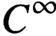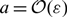Refine listing
Actions for selected content:
562 results in 35-XX
On the fractional Lazer-McKenna conjecture with critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 879-911
- Print publication:
- August 2022
-
- Article
- Export citation
Global well-posedness and nonlinear stability of a chemotaxis system modelling multiple sclerosis
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 28 July 2021, pp. 826-856
- Print publication:
- August 2022
-
- Article
- Export citation
Asymptotic stability of rarefaction wave for the compressible Navier‐Stokes‐Korteweg equations in the half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 756-779
- Print publication:
- June 2022
-
- Article
- Export citation
A NOTE ON THE AXISYMMETRIC DIFFUSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 21 July 2021, pp. 333-341
-
- Article
- Export citation
Invasion fronts and adaptive dynamics in a model for the growth of cell populations with heterogeneous mobility
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 766-783
-
- Article
- Export citation
Cahn–Hilliard equations on an evolving surface
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 937-1000
-
- Article
- Export citation
Asymptotics of the principal eigenvalue of the Laplacian in 2D periodic domains with small traps
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 04 June 2021, pp. 646-673
-
- Article
- Export citation
Concentration phenomena for fractional magnetic NLS equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 28 May 2021, pp. 479-517
- Print publication:
- April 2022
-
- Article
- Export citation
Estimate, existence and nonexistence of positive solutions of Hardy–Hénon equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 518-541
- Print publication:
- April 2022
-
- Article
- Export citation
Geometric series expansion of the Neumann–Poincaré operator: Application to composite materials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 560-585
-
- Article
- Export citation
Eigenoscillations in an angular domain and spectral properties of functional equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 06 May 2021, pp. 538-559
-
- Article
- Export citation
Linear evolution equations on the half-line with dynamic boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 505-537
-
- Article
- Export citation
UNIFORM LOWER BOUND AND LIOUVILLE TYPE THEOREM FOR FRACTIONAL LICHNEROWICZ EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 21 April 2021, pp. 484-492
- Print publication:
- December 2021
-
- Article
- Export citation
Dynamics of an infection age-space structured cholera model with Neumann boundary condition
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 393-422
-
- Article
- Export citation
Smoothness of solutions of a convolution equation of restricted type on the sphere
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 April 2021, e12
-
- Article
-
- You have access
- Open access
- Export citation
ASYMPTOTIC ANALYSIS FOR THE MEAN FIRST PASSAGE TIME IN FINITE OR SPATIALLY PERIODIC 2D DOMAINS WITH A CLUSTER OF SMALL TRAPS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1-22
-
- Article
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
- Print publication:
- April 2022
-
- Article
- Export citation
Spikes and localised patterns for a novel Schnakenberg model in the semi-strong interaction regime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 133-152
-
- Article
- Export citation
Modelling viscoelastic wave phenomenon by homogenisation of the poroelasticity equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 846-864
-
- Article
- Export citation
On a repulsion Keller–Segel system with a logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 153-181
-
- Article
- Export citation