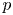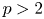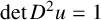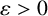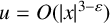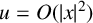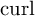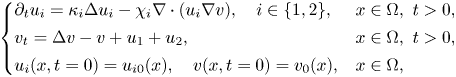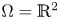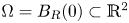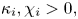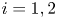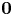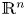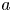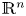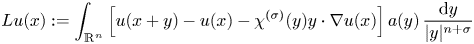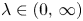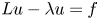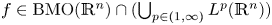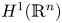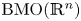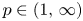Refine listing
Actions for selected content:
594 results in 35-XX
Local regularity for nonlinear elliptic and parabolic equations with anisotropic weights
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 391-436
-
- Article
- Export citation
Convergence for the fractional p-Laplacian and its application to the extended Nirenberg problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 660-672
- Print publication:
- April 2024
-
- Article
- Export citation
MODELS OF FLOW AND DIFFUSION: SELECTIVE WITHDRAWAL FROM A STRATIFIED FLUID AND DISPERSAL OF HYDROGEN IN THE RETINA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 520-521
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
THE GROWTH OF SOLUTIONS OF MONGE–AMPÈRE EQUATIONS IN HALF SPACES AND ITS APPLICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 31 March 2023, pp. 125-137
- Print publication:
- February 2024
-
- Article
- Export citation
Vanishing limit for the three-dimensional incompressible Phan-Thien–Tanner system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 673-698
- Print publication:
- June 2024
-
- Article
- Export citation
Partial Euler operators and the efficient inversion of Div
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 20 March 2023, pp. 1046-1066
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solvability for Pucci-Lane-Emden systems in annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 494-507
- Print publication:
- April 2024
-
- Article
- Export citation
COMPACTNESS AND STRUCTURE OF ZERO-STATES FOR UNORIENTED AVILES–GIGA FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 941-982
- Print publication:
- March 2024
-
- Article
- Export citation
Existence of weak solutions to an anisotropic parabolic–parabolic chemotaxis system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 424-444
- Print publication:
- April 2024
-
- Article
- Export citation
Dimension reduction analysis of a three-dimensional thin elastic plate reinforced with fractal ribbons
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 02 March 2023, pp. 838-869
-
- Article
- Export citation
Global classical solution to the chemotaxis-Navier-Stokes system with some realistic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 March 2023, pp. 445-482
- Print publication:
- April 2024
-
- Article
- Export citation
Asymptotic profiles for positive solutions of diffusive logistic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 February 2023, pp. 273-284
- Print publication:
- February 2024
-
- Article
- Export citation
A note on energy equality for the fractional Navier-Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 February 2023, pp. 201-208
- Print publication:
- February 2024
-
- Article
- Export citation
A homogenised model for the motion of evaporating fronts in porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 806-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant Galton–Watson trees: metric properties and attraction with respect to generalized dynamical pruning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 643-671
- Print publication:
- June 2023
-
- Article
- Export citation
On the global existence of solutions to chemotaxis system for two populations in dimension two
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 2106-2128
- Print publication:
- December 2023
-
- Article
- Export citation
Two approximate symmetry frameworks for nonlinear partial differential equations with a small parameter: Comparisons, relations, approximate solutions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 16 December 2022, pp. 1017-1045
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
Symmetry via the moving plane method for a class of quasilinear elliptic problems involving the Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1858-1882
- Print publication:
- December 2023
-
- Article
- Export citation
Global optimisation of the mean first passage time for narrow capture problems in elliptic domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 1269-1287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation