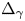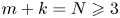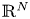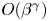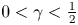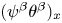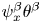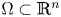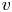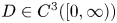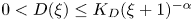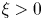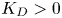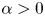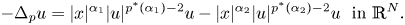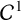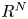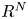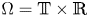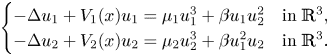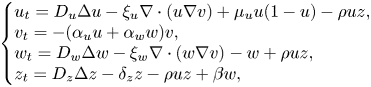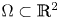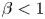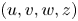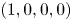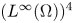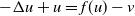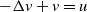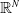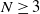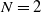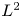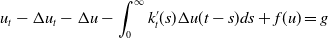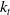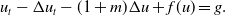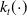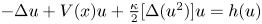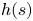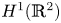Refine listing
Actions for selected content:
593 results in 35-XX
A Berestycki–Lions type result for a class of degenerate elliptic problems involving the Grushin operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 1244-1271
- Print publication:
- August 2023
-
- Article
- Export citation
On a class of critical N-Laplacian problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 27 June 2022, pp. 556-576
-
- Article
- Export citation
Homogenisation of a two-phase problem with nonlinear dynamic Wentzell-interface condition for connected–disconnected porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 617-641
-
- Article
- Export citation
Boundary layer of Hsieh's equation with conservative nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1167-1197
- Print publication:
- August 2023
-
- Article
- Export citation
Finite-time blow-up in a repulsive chemotaxis-consumption system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1150-1166
- Print publication:
- August 2023
-
- Article
- Export citation
The ground states of quasilinear Hénon equation with double weighted critical exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 June 2022, pp. 1037-1044
- Print publication:
- June 2023
-
- Article
- Export citation
REGULARITY OF AML FUNCTIONS IN TWO-DIMENSIONAL NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 406-430
-
- Article
- Export citation
LOG-TRANSFORM AND THE WEAK HARNACK INEQUALITY FOR KINETIC FOKKER-PLANCK EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 2749-2774
- Print publication:
- November 2023
-
- Article
- Export citation
Fractional interpolation inequality and radially symmetric ground states
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 937-957
- Print publication:
- June 2023
-
- Article
- Export citation
Stability and exponential decay for magnetohydrodynamic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 853-880
- Print publication:
- June 2023
-
- Article
- Export citation
Non-degeneracy of synchronized vector solutions for weakly coupled nonlinear schrödiner systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 22 April 2022, pp. 441-459
-
- Article
- Export citation
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 881-906
- Print publication:
- June 2023
-
- Article
- Export citation
A pinching estimate for convex hypersurfaces evolving under a non-homogeneous variant of mean curvature flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 376-391
-
- Article
- Export citation
Existence of solution for a class of activator–inhibitor systems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 April 2022, pp. 98-113
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Corrigendum: Dynamics of a susceptible—infected—susceptible epidemic reaction—diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 718-720
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 764-783
- Print publication:
- June 2023
-
- Article
- Export citation
ELECTRICAL IMPEDANCE TOMOGRAPHY USING NONCONFORMING MESH AND POSTERIOR APPROXIMATED REGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 520-522
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
The nonclassical diffusion equations with time-dependent memory kernels and a new class of nonlinearities
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 February 2022, pp. 716-733
-
- Article
- Export citation
Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 279-301
-
- Article
- Export citation