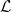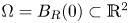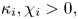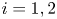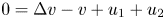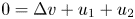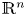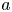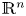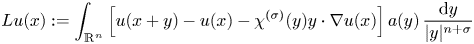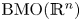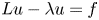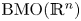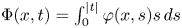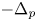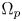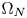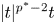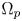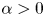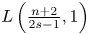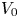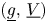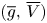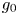Refine listing
Actions for selected content:
562 results in 35-XX
A note on energy equality for the fractional Navier-Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 February 2023, pp. 201-208
- Print publication:
- February 2024
-
- Article
- Export citation
A homogenised model for the motion of evaporating fronts in porous media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 806-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant Galton–Watson trees: metric properties and attraction with respect to generalized dynamical pruning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 643-671
- Print publication:
- June 2023
-
- Article
- Export citation
On the global existence of solutions to chemotaxis system for two populations in dimension two
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 2106-2128
- Print publication:
- December 2023
-
- Article
- Export citation
Two approximate symmetry frameworks for nonlinear partial differential equations with a small parameter: Comparisons, relations, approximate solutions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 16 December 2022, pp. 1017-1045
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
Symmetry via the moving plane method for a class of quasilinear elliptic problems involving the Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1858-1882
- Print publication:
- December 2023
-
- Article
- Export citation
Global optimisation of the mean first passage time for narrow capture problems in elliptic domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 1269-1287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact nonclassical symmetry solutions of Lotka–Volterra-type population systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 998-1016
-
- Article
- Export citation
Dirichlet vs Neumann
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1063-1074
-
- Article
- Export citation
Symmetry actions and brackets for adjoint-symmetries. II: Physical examples
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 21 November 2022, pp. 974-997
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some results for semi-stable radial solutions of k-Hessian equations with weight on ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 1751-1776
- Print publication:
- October 2023
-
- Article
- Export citation
Existence and stability of singular patterns in a fractional Ginzburg–Landau equation with a mean field
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1242-1268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hölder regularity and Liouville properties for nonlinear elliptic inequalities with power-growth gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 1833-1857
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hardy–Littlewood–Sobolev inequality and existence of the extremal functions with extended kernel
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 31 October 2022, pp. 1683-1705
- Print publication:
- October 2023
-
- Article
- Export citation
Multiple solutions for a class of quasilinear problems with double criticality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 October 2022, pp. 1011-1047
-
- Article
- Export citation
Symmetry actions and brackets for adjoint-symmetries. I: Main results and applications
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 October 2022, pp. 947-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borderline gradient continuity for fractional heat type operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 1651-1682
- Print publication:
- October 2023
-
- Article
- Export citation
Local well-posedness and global analyticity for solutions of a generalized 0-equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 1630-1650
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the optimization of the first weighted eigenvalue
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 1777-1804
- Print publication:
- December 2023
-
- Article
- Export citation