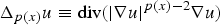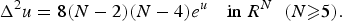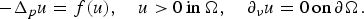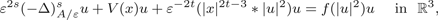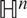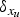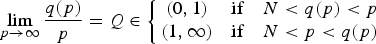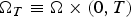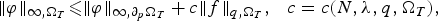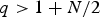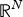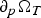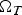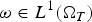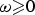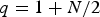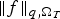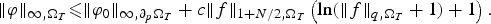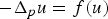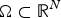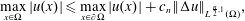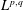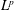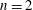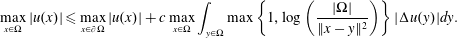Refine listing
Actions for selected content:
562 results in 35-XX
A p(x)-Laplacian extension of the Díaz-Saa inequality and some applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 205-232
- Print publication:
- February 2020
-
- Article
- Export citation
Non-collapsing in homogeneity greater than one via a two-point method for a special case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1627-1635
- Print publication:
- December 2019
-
- Article
- Export citation
Radial symmetry of non-maximal entire solutions of a bi-harmonic equation with exponential nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1603-1625
- Print publication:
- December 2019
-
- Article
- Export citation
A priori bounds and multiplicity of positive solutions for p-Laplacian Neumann problems with sub-critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 73-102
- Print publication:
- February 2020
-
- Article
- Export citation
Multiplicity and concentration results for a fractional Schrödinger-Poisson type equation with magnetic field
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 655-694
- Print publication:
- April 2020
-
- Article
- Export citation
Long-time asymptotic expansions for Navier-Stokes equations with power-decaying forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 569-606
- Print publication:
- April 2020
-
- Article
- Export citation
A CLASS OF CRITICAL KIRCHHOFF PROBLEM ON THE HYPERBOLIC SPACE
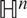 $\mathbb{H}^{{\it n}}$
$\mathbb{H}^{{\it n}}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 January 2019, pp. 109-122
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On critical exponents of a k-Hessian equation in the whole space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1555-1575
- Print publication:
- December 2019
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
- Print publication:
- December 2019
-
- Article
- Export citation
Complete quenching phenomenon and instantaneous shrinking of support of solutions of degenerate parabolic equations with nonlinear singular absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1323-1346
- Print publication:
- October 2019
-
- Article
- Export citation
Infinite multiplicity of stable entire solutions for a semilinear elliptic equation with exponential nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1371-1404
- Print publication:
- October 2019
-
- Article
- Export citation
On the classification of standing wave solutions to a coupled Schrödinger system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1347-1370
- Print publication:
- October 2019
-
- Article
- Export citation
Converge rates towards stationary solutions for the outflow problem of planar magnetohydrodynamics on a half line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1291-1322
- Print publication:
- October 2019
-
- Article
- Export citation
Strong maximum principles for fractional Laplacians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1223-1240
- Print publication:
- October 2019
-
- Article
- Export citation
Logarithmic upper bounds for weak solutions to a class of parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1481-1491
- Print publication:
- December 2019
-
- Article
- Export citation
On a property of the nodal set of least energy sign-changing solutions for quasilinear elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1163-1173
- Print publication:
- October 2019
-
- Article
- Export citation
An Endpoint Alexandrov Bakelman Pucci Estimate in the Plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 643-651
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
ANALYTIC HYPOELLIPTICITY FOR SUMS OF SQUARES IN THE PRESENCE OF SYMPLECTIC NON TREVES STRATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1877-1888
- Print publication:
- November 2020
-
- Article
- Export citation
Existence of travelling waves with the critical speed for an influenza model with treatment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 232-245
-
- Article
- Export citation
A Note About the Strong Maximum Principle on RCD Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 259-266
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation