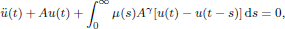Refine listing
Actions for selected content:
562 results in 35-XX
On The Uniqueness of Solutions for Kawahara Type Equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 623-646
-
- Article
- Export citation
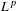 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 231-258
- Print publication:
- January 2020
-
- Article
- Export citation
Hardy-Type Inequalities for Fractional Powers of the Dunkl–Hermite Operator
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 513-544
-
- Article
- Export citation
CALCULATION OF CRITICAL PARAMETERS FOR SPONTANEOUS COMBUSTION FOR SOME COMPLEX GEOMETRIES USING AN INDIRECT NUMERICAL METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 3 / January 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 402-412
-
- Article
-
- You have access
- Export citation
On the Harnack inequality for quasilinear elliptic equations with a first-order term
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 February 2018, pp. 1075-1095
- Print publication:
- October 2018
-
- Article
- Export citation
Evolution of non-simple closed curves in the area-preserving curvature flow
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 659-668
- Print publication:
- June 2018
-
- Article
- Export citation
EXISTENCE OF TRAVELLING WAVES IN THE FRACTIONAL BURGERS EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 102-109
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Normalized solutions for nonlinear Schrödinger systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 November 2017, pp. 225-242
- Print publication:
- April 2018
-
- Article
- Export citation
Existence of travelling-wave solutions representing domain wall motion in a thin ferromagnetic nanowire
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 395-407
- Print publication:
- April 2018
-
- Article
- Export citation
Infinitely many non-radial singular solutions of
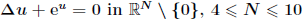
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 133-147
- Print publication:
- February 2018
-
- Article
- Export citation
Infinitely many solutions for three classes of self-similar equations with p-Laplace operator: Gelfand, Joseph–Lundgren and MEMS problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 341-356
- Print publication:
- April 2018
-
- Article
- Export citation
A FUJITA-TYPE RESULT FOR A SEMILINEAR EQUATION IN HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 420-429
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Stability of line solitons for the KP-II equation in ℝ2. II
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 September 2017, pp. 149-198
- Print publication:
- February 2018
-
- Article
- Export citation
Learning Non-Negativity Constrained Variation for Image Denoising and Deblurring
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 852-871
- Print publication:
- November 2017
-
- Article
- Export citation
Some sharp results about the global existence and blowup of solutions to a class of pseudo-parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1311-1331
- Print publication:
- December 2017
-
- Article
- Export citation
Primal-Dual Active Set Method for American Lookback Put Option Pricing
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 603-614
- Print publication:
- August 2017
-
- Article
- Export citation
Finite speed of propagation and waiting time for a thin-film Muskat problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 813-830
- Print publication:
- August 2017
-
- Article
- Export citation
Positive solutions of Kirchhoff-type non-local elliptic equation: a bifurcation approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 875-894
- Print publication:
- August 2017
-
- Article
- Export citation
Stability analysis for positive solutions for classes of semilinear elliptic boundary-value problems with nonlinear boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 1019-1040
- Print publication:
- October 2017
-
- Article
- Export citation
The lack of exponential stability for a class of second-order systems with memory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 683-702
- Print publication:
- August 2017
-
- Article
- Export citation
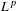
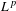
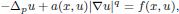

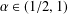
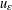
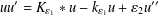
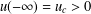
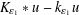
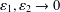
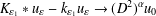
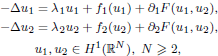
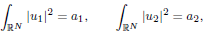
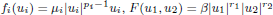 , with positive constants
, with positive constants 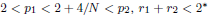 in dimensions 2 ≤
in dimensions 2 ≤