In this paper we deal with a singular elliptic problem involving an asymptotically linear nonlinearity and depending on two positive parameters. We investigate the existence, uniqueness and non-existence of the minima of the functional associated with the problem and, by employing a natural and very general definition of a weak solution, we also obtain a bifurcation-type result.

We are interested in entire solutions for the semilinear biharmonic equation Δ2 u = f(u) in ℝN , where f(u) = eu or –u –p (p > 0). For the exponential case, we prove that for the polyharmonic problem Δ2m u = eu with positive integer m, any classical entire solution verifies Δ2m–1 u < 0; this completes the results of Dupaigne et al. (Arch. Ration. Mech. Analysis208 (2013), 725–752) and Wei and Xu (Math. Annalen313 (1999), 207–228). We also obtain a refined asymptotic expansion of the radial separatrix solution to Δ2 u = eu in ℝ3, which answers a question posed by Berchio et al. (J. Diff. Eqns252 (2012), 2569–2616). For the negative power case, we show the non-existence of the classical entire solution for any 0 < p ⩽ 1.

Consider the (elliptic) stationary nonlinear reaction–diffusion equation in a sequence of bounded Neumann tubes in a space that is squeezed to a reference curve. It is supposed that the forcing term is square integrable and that the nonlinear one satisfies some growth and dissipative conditions. A norm convergence of the resolvents of the operators associated with the linear terms of such equations is proven, and this fact is used to provide new and simpler proofs of the asymptotic behaviour of the solutions to the full nonlinear equations (previously known in similar singular problems).

We incorporate the new theory of equivariant moving frames for Lie pseudogroups into Vessiot’s method of group foliation of differential equations. The automorphic system is replaced by a set of reconstruction equations on the pseudogroup jets. The result is a completely algorithmic and symbolic procedure for finding both invariant and noninvariant solutions of differential equations admitting a symmetry group.

In this work we study the homogenisation problem for nonlinear elliptic equations involving $p$-Laplacian-type operators with sign-changing weights. We study the asymptotic behaviour of variational eigenvalues which consist of a double sequence of eigenvalues. We show that the $k$th positive eigenvalue goes to infinity when the average of the weights is nonpositive, and converges to the $k$th variational eigenvalue of the limit problem when the average is positive for any $k\geq 1$.

When an incident Herglotz wave function scatters from a periodic Lipschitz continuous surface with a Dirichlet boundary condition, the classical (quasi-)periodic solution theory for scattering from periodic structures does not apply, since the incident field lacks periodicity. Relying on the Bloch transform, we provide a solution theory in H1 for this scattering problem. First, we prove conditions guaranteeing that incident Herglotz wave functions propagating towards the periodic structure have traces in H1/2 on the periodic surface. Second, we show that the solution to the scattering problem can be decomposed by the Bloch transform into periodic components that solve a periodic scattering problem. Third, these periodic solutions yield an equivalent characterization of the solution to the original non-periodic scattering problem, which allows, for instance, new characterizations of the Rayleigh coefficients of each of the periodic components to be shown. A corollary of our results is that under the conditions mentioned above the operator that maps densities to the restriction of their Herglotz wave function on the periodic surface is always injective; this result generally fails for bounded surfaces.

We study the multiplicity and concentration behaviour of positive solutions for a quasi-linear Choquard equation

where Δp is the p-Laplacian operator, 1 < p < N, V is a continuous real function on ℝN , 0 < μ < N, F(s) is the primitive function of f(s), ε is a positive parameter and * represents the convolution between two functions. The question of the existence of semiclassical solutions for the semilinear case p = 2 has recently been posed by Ambrosetti and Malchiodi. We suppose that the potential satisfies the condition introduced by del Pino and Felmer, i.e.V has a local minimum. We prove the existence, multiplicity and concentration of solutions for the equation by the penalization method and Lyusternik–Schnirelmann theory and even show novel results for the semilinear case p = 2.

We present a new method for investigating the Lp -type pullback attractors (2 ≤ p < ∞) of a semilinear heat equation on a time-varying domain under quite general assumptions on the nonlinear and forcing terms. The existing approach does not appear applicable here as it is impossible to show the existence of a pullback absorbing set in Lp space when p is large. A new asymptotic decomposition scheme for a non-autonomous pullback attractor has been introduced. The abstract results and preliminary lemmas are also of independent interest and applicable to other systems.

We prove the linear and nonlinear instability of periodic traveling wave solutions for a generalized version of the symmetric regularized long wave (SRLW) equation. Using analytic and asymptotic perturbation theory, we establish sufficient conditions for the existence of exponentially growing solutions to the linearized problem and so the linear instability of periodic profiles is obtained. An application of this approach is made to obtain the linear/nonlinear instability of cnoidal wave solutions for the modified SRLW (mSRLW) equation. We also prove the stability of dnoidal wave solutions associated to the equation just mentioned.

This paper is concerned with the existence, non-existence and qualitative properties of cylindrically symmetric travelling fronts for time-periodic reaction–diffusion equations with bistable nonlinearity in ℝm with m ≥ 2. It should be mentioned that the existence and stability of two-dimensional time-periodic V-shaped travelling fronts and three-dimensional time-periodic pyramidal travelling fronts have been studied previously. In this paper we consider two cases: the first is that the wave speed of a one-dimensional travelling front is positive and the second is that the one-dimensional wave speed is zero. For both cases we establish the existence, non-existence and qualitative properties of cylindrically symmetric travelling fronts. In particular, for the first case we furthermore show the asymptotic behaviours of level sets of the cylindrically symmetric travelling fronts.

This paper is concerned with the asymptotic behaviour of solutions to quasilinear hyperbolic equations with nonlinear damping on the quarter-plane (x, t) ∈ ℝ+ x ∈ ℝ+. We obtain the Lp (1 ≤ p ≤ +∞) convergence rates of the solution to the quasilinear hyperbolic equations without the additional technical assumptions for the nonlinear damping f(v) given by Li and Saxton.

We establish a sharp ultimate bound of the solution to a second-order dissipative nonlinear equation with bounded forcing term.

The paper deals with blow-up for the solutions of an evolution problem consisting in a semilinear wave equation posed in a bounded C1,1 open subset of ℝn, supplied with a Neumann boundary condition involving a nonlinear dissipation. The typical problem studied is

where ∂Ω = Γ0 ∪ Γ1, Γ0 ∩ Γ1 = ∅, σ(Γ0) > 0, 2 < p ≤ 2(n − 1)/(n − 2) (when n ≥ 3), m > 1, α ∈ L∞(Γ1), α ≥ 0 and β ≥ 0. The initial data are posed in the energy space.The aim of the paper is to improve previous blow-up results concerning the problem.

We study non-autonomous parabolic equations with critical exponents in a scale of Banach spaces Eσ, σ ∈ [0,1 + μ). We consider a suitable E1+ε-solution and describe continuation properties of the solution. This concerns both a situation when the solution can be continued as an E1+ε-solution and a situation when the E1+ε-norm of the solution blows up, in which case a piecewise E1+ε-solution is constructed.

We investigate the decay for |x|→∞ of weak Sobolev-type solutions of semilinear nonlocal equations Pu = F(u). We consider the case when P = p(D) is an elliptic Fourier multiplier with polyhomogeneous symbol p(ξ), and we derive algebraic decay estimates in terms of weighted Sobolev norms. Our basic example is the celebrated Benjamin–Ono equation

for internal solitary waves of deep stratified fluids. Their profile presents algebraic decay, in strong contrast with the exponential decay for KdV shallow water waves.

We consider the first boundary value problem for a second-order parabolic equation with variable coefficients in the domain $K\times \mathbb{R}^{n-m}$, where $K$ is an $m$-dimensional cone. The main results of the paper are pointwise estimates of the Green’s function.

We introduce a novel solution concept, denoted ${\it\alpha}$-dissipative solutions, that provides a continuous interpolation between conservative and dissipative solutions of the Cauchy problem for the two-component Camassa–Holm system on the line with vanishing asymptotics. All the ${\it\alpha}$-dissipative solutions are global weak solutions of the same equation in Eulerian coordinates, yet they exhibit rather distinct behavior at wave breaking. The solutions are constructed after a transformation into Lagrangian variables, where the solution is carefully modified at wave breaking.

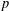
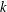
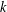
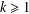
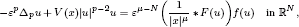
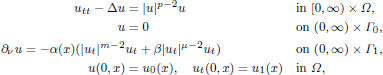
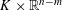
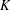
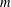
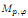We prove continuity in generalized parabolic Morrey spaces of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global -regularity result for the Cauchy—Dirichlet problem for linear uniformly parabolic equations with vanishing mean oscillation (VMO) coefficients.

During the past 55 years substantial progress concerning sharp constants in Poincaré-type and Steklov-type inequalities has been achieved. Original results of H. Poincaré, V. A. Steklov and his disciples are reviewed along with the main further developments in this area.