Refine listing
Actions for selected content:
562 results in 35-XX
ON A CLASS OF ELLIPTIC SYSTEM OF SCHRÖDINGER–POISSON TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 301-314
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A POSITIVE SOLUTION FOR A NONLOCAL SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 15 July 2014, pp. 469-475
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Existence, Stability and Oscillation Properties of Slow-Decay Positive Solutions of Supercritical Elliptic Equations with Hardy Potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 16 April 2014, pp. 255-271
-
- Article
-
- You have access
- Export citation
Poincaré–Lelong equation via the Hodge–Laplace heat equation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 1856-1870
- Print publication:
- November 2013
-
- Article
- Export citation
SOME REMARKS ON THE PIGOLA–RIGOLI–SETTI VERSION OF THE OMORI–YAU MAXIMUM PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 19 August 2013, pp. 337-342
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Microlocal Euler classes and Hochschild homology
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 487-516
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON RESOLVENT CONVERGENCE ON A THIN DOMAIN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 June 2013, pp. 141-148
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
CRITICAL TIMESCALES AND TIME INTERVALS FOR COUPLED LINEAR PROCESSES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 22 April 2013, pp. 127-142
-
- Article
-
- You have access
- Export citation
Microlocal defect measures for a degenerate thermoelasticity system
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 17 April 2013, pp. 145-181
- Print publication:
- January 2014
-
- Article
- Export citation
Compactness properties of critical nonlinearities and nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 05 April 2013, pp. 427-441
-
- Article
-
- You have access
- Export citation
HOMOGENIZATION OF THE DIRICHLET PROBLEM FOR ELLIPTIC SYSTEMS:
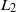 $L_2$-OPERATOR ERROR ESTIMATES
$L_2$-OPERATOR ERROR ESTIMATES
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 01 February 2013, pp. 463-476
- Print publication:
- July 2013
-
- Article
- Export citation
MASS CONCENTRATION WITH MIXED NORM FOR A NONELLIPTIC SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 March 2013, pp. 238-258
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
SEIBERG–WITTEN FLOW IN HIGHER DIMENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 311-324
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
ON THE GROUND STATE OF SPIN-1 BOSE–EINSTEIN CONDENSATES WITH AN EXTERNAL IOFFE–PITCHARD MAGNETIC FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 28 May 2012, pp. 356-369
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
A result of multiplicity of solutions for a class of quasilinear equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 291-309
-
- Article
-
- You have access
- Export citation
Multiplicity of solutions to the weighted critical quasilinear problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 181-195
-
- Article
-
- You have access
- Export citation
Dimension reduction and homogenization of random degenerate operators. Part I
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 January 2012, pp. 1-22
-
- Article
-
- You have access
- Export citation
DOMAIN PERTURBATION FOR PARABOLIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 174-176
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Convexity-preserving flows of totally competitive planar Lotka–Volterra equations and the geometry of the carrying simplex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 53-63
-
- Article
-
- You have access
- Export citation
INHOMOGENEOUS PERIODIC PARABOLIC PROBLEMS WITH INDEFINITE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 516-524
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
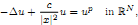
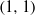
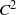
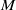
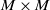
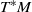
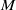
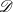
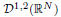 and
and 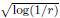 of the respective Hardy-type inequalities, as well as compactness of the limiting Sobolev embeddings once the Sobolev norm is appended by a potential term whose growth at singularities exceeds that of the corresponding Hardy-type potential.
of the respective Hardy-type inequalities, as well as compactness of the limiting Sobolev embeddings once the Sobolev norm is appended by a potential term whose growth at singularities exceeds that of the corresponding Hardy-type potential.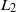
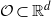
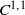
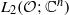
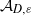
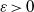
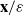
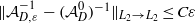
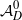
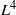
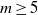
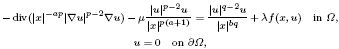
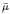 ≡ ((
≡ ((