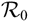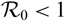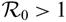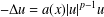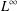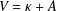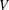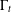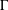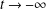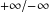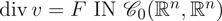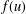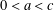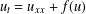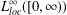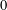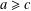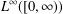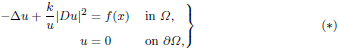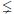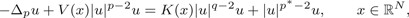Refine listing
Actions for selected content:
562 results in 35-XX
MICROLOCAL REGULARITY FOR MIZOHATA TYPE DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1185-1209
- Print publication:
- July 2020
-
- Article
- Export citation
Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 26-56
-
- Article
- Export citation
The time-dependent Schrödinger equation with piecewise constant potentials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 57-83
-
- Article
- Export citation
Asymptotic and transient behaviour for a nonlocal problem arising in population genetics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 84-110
-
- Article
- Export citation
Three Solutions for a Singular Quasilinear Elliptic Problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 179-196
-
- Article
- Export citation
A Class of Fourth Order Damped Wave Equations with Arbitrary Positive Initial Energy
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 165-178
-
- Article
- Export citation
TWO-SIDED ESTIMATES FOR POSITIVE SOLUTIONS OF SUPERLINEARELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 465-473
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 137-147
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
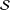 ${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 456-464
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Solving the Equation
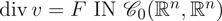 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1055-1061
-
- Article
- Export citation
Existence and Concentration of Positive Solutions for Nonlinear Kirchhoff-Type Problems with a General Critical Nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1023-1040
-
- Article
- Export citation
Optimal stability estimates for continuity equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 16 July 2018, pp. 1279-1296
- Print publication:
- December 2018
-
- Article
- Export citation
A REACTION–DIFFUSION–ADVECTION EQUATION WITH COMBUSTION NONLINEARITY ON THE HALF-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 02 July 2018, pp. 277-285
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
A uniqueness result for a singular elliptic equation with gradient term
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 983-994
- Print publication:
- October 2018
-
- Article
- Export citation
Quasilinear Scalar Field Equations Involving Critical Sobolev Exponents and Potentials Vanishing at Infinity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 30 April 2018, pp. 705-733
-
- Article
- Export citation
ON SYSTEMS OF PARTIAL DIFFERENTIAL EQUATIONS OF BRIOT–BOUQUET TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 122-133
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Sharp decay estimates in a bioconvection model with quadratic degradation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 939-955
- Print publication:
- October 2018
-
- Article
- Export citation
Classification of extinction profiles for a one-dimensional diffusive Hamilton–Jacobi equation with critical absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 559-574
- Print publication:
- June 2018
-
- Article
- Export citation
Poincaré inequalities for Sobolev spaces with matrix-valued weights and applications to degenerate partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 April 2018, pp. 61-100
- Print publication:
- February 2019
-
- Article
- Export citation
Time-dependent attractors for non-autonomous non-local reaction–diffusion equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 957-981
- Print publication:
- October 2018
-
- Article
- Export citation